Question

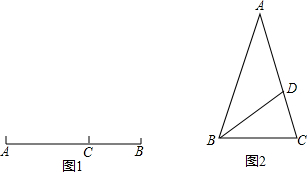（2013•莆田）定义：如图1，点C在线段AB上，若满足AC²=BC•AB，则称点C为线段AB的黄金分割点．
如图2，△ABC中，AB=AC=1，∠A=36°，BD平分∠ABC交AC于点D．
（1）求证：点D是线段AC的黄金分割点；
（2）求出线段AD的长．

Answer 1

分析：（1）判断△ABC∽△BDC，根据对应边成比例可得出答案．
（2）根据黄金比值即可求出AD的长度．

解答：解：（1）∵∠A=36°，AB=AC，
∴∠ABC=∠ACB=72°，
∵BD平分∠ABC，
∴∠CBD=∠ABD=36°，∠BDC=72°，
∴AD=BD，BC=BD，
∴△ABC∽△BDC，
∴

BD

AB

=

CD

BC

，即

AD

AC

=

CD

AD

，
∴AD²=AC•CD．
∴点D是线段AC的黄金分割点．

（2）∵点D是线段AC的黄金分割点，
∴AD=

5 -1

2

AC，
∵AC=1，
∴AD=

5 -1

2

．

点评：本题考查了黄金分割的知识，解答本题的关键是仔细审题，理解黄金分割的定义，注意掌握黄金比值．