题目内容
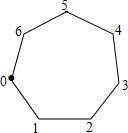 (2012•永州)如图,一枚棋子放在七角棋盘的第0号角,现依逆时针方向移动这枚棋子,其各步依次移动1,2,3,…,n个角,如第一步从0号角移动到第1号角,第二步从第1号角移动到第3号角,第三步从第3号角移动到第6号角,….若这枚棋子不停地移动下去,则这枚棋子永远不能到达的角的个数是( )
(2012•永州)如图,一枚棋子放在七角棋盘的第0号角,现依逆时针方向移动这枚棋子,其各步依次移动1,2,3,…,n个角,如第一步从0号角移动到第1号角,第二步从第1号角移动到第3号角,第三步从第3号角移动到第6号角,….若这枚棋子不停地移动下去,则这枚棋子永远不能到达的角的个数是( )分析:因棋子移动了k次后走过的总格数是1+2+3+…+k=
k(k+1),然后根据题目中所给的第k次依次移动k个顶点的规则,可得到不等式最后求得解.
| 1 |
| 2 |
解答:解:因棋子移动了k次后走过的总格数是1+2+3+…+k=
k(k+1),应停在第
k(k+1)-7p格,
这时P是整数,且使0≤
k(k+1)-7p≤6,分别取k=1,2,3,4,5,6,7时,
k(k+1)-7p=1,3,6,3,1,0,0,发现第2,4,5格没有停棋,
若7<k≤10,设k=7+t(t=1,2,3)代入可得,
k(k+1)-7p=7m+
t(t+1),
由此可知,停棋的情形与k=t时相同,
故第2,4,5格没有停棋,
即:这枚棋子永远不能到达的角的个数是3.
故选D.
| 1 |
| 2 |
| 1 |
| 2 |
这时P是整数,且使0≤
| 1 |
| 2 |
| 1 |
| 2 |
若7<k≤10,设k=7+t(t=1,2,3)代入可得,
| 1 |
| 2 |
| 1 |
| 2 |
由此可知,停棋的情形与k=t时相同,
故第2,4,5格没有停棋,
即:这枚棋子永远不能到达的角的个数是3.
故选D.
点评:本题考查理解题意能力,关键是知道棋子所停的规则,找到规律,然后得到不等式求解.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 (2012•永州)如图,已知圆O的半径为4,∠A=45°,若一个圆锥的侧面展开图与扇形OBC能完全重合,则该圆锥的底面圆的半径为
(2012•永州)如图,已知圆O的半径为4,∠A=45°,若一个圆锥的侧面展开图与扇形OBC能完全重合,则该圆锥的底面圆的半径为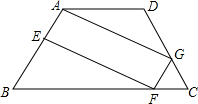 (2012•永州)如图,在等腰梯形ABCD中,AD∥BC,点E、F、G分别在边AB、BC、CD上,且AE=GF=GC.求证:四边形AEFG为平行四边形.
(2012•永州)如图,在等腰梯形ABCD中,AD∥BC,点E、F、G分别在边AB、BC、CD上,且AE=GF=GC.求证:四边形AEFG为平行四边形.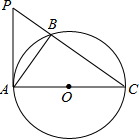 (2012•永州)如图,AC是⊙O的直径,PA是⊙O的切线,A为切点,连接PC交⊙O于点B,连接AB,且PC=10,PA=6.
(2012•永州)如图,AC是⊙O的直径,PA是⊙O的切线,A为切点,连接PC交⊙O于点B,连接AB,且PC=10,PA=6. 过点(0,-2)且与x轴平行的直线,P(m,n)是该二次函数图象上的任意一点,过P作PH⊥l,H为垂足.
过点(0,-2)且与x轴平行的直线,P(m,n)是该二次函数图象上的任意一点,过P作PH⊥l,H为垂足.