题目内容
一元二次方程（1-k）x2-2x-1=0有两个不相等的实数根，则k的取值范围是（ ）A．k＞2
B．k＜2且k≠1
C．k＜2
D．k＞2且k≠1
【答案】分析：在与一元二次方程有关的求值问题中，必须满足下列条件：
（1）二次项系数不为零；
（2）在有不相等的实数根下必须满足△=b2-4ac＞0．
解答：解：∵a=1-k，b=-2，c=-1，一元二次方程有两个不相等的实数根，
∴△=b2-4ac=22-4×（1-k）×（-1）＞0，解得k＜2，
∵（1-k）是二次项系数，不能为0，
∴k≠1且k＜2．
故选B．
点评：本题考查了一元二次方程根的判别式的应用．切记不要忽略一元二次方程二次项系数不为零这一隐含条件．
（1）二次项系数不为零；
（2）在有不相等的实数根下必须满足△=b2-4ac＞0．
解答：解：∵a=1-k，b=-2，c=-1，一元二次方程有两个不相等的实数根，
∴△=b2-4ac=22-4×（1-k）×（-1）＞0，解得k＜2，
∵（1-k）是二次项系数，不能为0，
∴k≠1且k＜2．
故选B．
点评：本题考查了一元二次方程根的判别式的应用．切记不要忽略一元二次方程二次项系数不为零这一隐含条件．
练习册系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
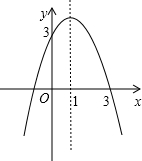已知二次函数y=-x2+bx+c的图象如图所示，解决下列问题：
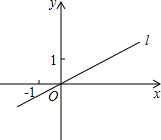如图，在平面直角坐标系中，直线l的解析式为y=