题目内容
三角形两边长分别是8和6,第三边长是一元二次方程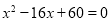 一个实数根,则该三角形的面积是( )
一个实数根,则该三角形的面积是( )
A.24 B.48 C.24或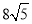 D.
D.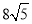
C.
【解析】
试题分析:由 ,得到
,得到 ,∴
,∴ 或
或 .
.
当 时,该三角形为以6为腰,8为底的等腰三角形.∴高h=
时,该三角形为以6为腰,8为底的等腰三角形.∴高h= ,
,
∴S△= ;
;
当 时,该三角形为以6和8为直角边,10为斜边的直角三角形.
时,该三角形为以6和8为直角边,10为斜边的直角三角形.
∴S△= .∴S=24或
.∴S=24或 .
.
故选:C.
考点:1.一元二次方程的应用;2.三角形三边关系;3.等腰三角形的性质.
考点分析: 考点1:一元二次方程 定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
一元二次方程的一般形式:

它的特征是:等式左边是一个关于未知数x的二次多项式,等式右边是零,其中 ax2叫做二次项,a叫做二次项系数;bx叫做一次项,b叫做一次项系数;c叫做常数项。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的顶点坐标是( )
的顶点坐标是( )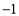 ,3) C.(1,
,3) C.(1,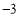 ) D.(
) D.( ,
,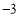 )
)
 在平面直角坐标系中的位置如图所示,其中A(1, 2),B(1, 1),C(3, 1),将△
在平面直角坐标系中的位置如图所示,其中A(1, 2),B(1, 1),C(3, 1),将△ 顺时针旋转
顺时针旋转 后得到△
后得到△ ,则点A旋转到点
,则点A旋转到点 所经过的路线长为( )
所经过的路线长为( )
 B.
B. C.
C. D.
D.

 其中,x=—3(6分)
其中,x=—3(6分) D.
D.