题目内容
如图，A、B、C是⊙O上的三个点，若∠C=35°，则∠OAB的度数是
- A.35°
- B.55°
- C.65°
- D.70°
B
分析：先根据圆周角定理求出∠AOB的度数，再由等腰三角形的性质及三角形内角和定理即可得出结论．
解答：∵∠AOB与∠C是同弧所对的圆心角与圆周角，
∴∠AOB=2∠C=2×35°=70°，
∵OA=OB，
∴∠OAB=∠OBA=
=
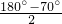=55°．
故选B．
点评：本题考查的是圆周角定理、等腰三角形的性质，解答此类题目时往往用到三角形的内角和是180°这一隐含条件．
分析：先根据圆周角定理求出∠AOB的度数，再由等腰三角形的性质及三角形内角和定理即可得出结论．
解答：∵∠AOB与∠C是同弧所对的圆心角与圆周角，
∴∠AOB=2∠C=2×35°=70°，
∵OA=OB，
∴∠OAB=∠OBA=
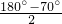==55°．故选B．
点评：本题考查的是圆周角定理、等腰三角形的性质，解答此类题目时往往用到三角形的内角和是180°这一隐含条件．
练习册系列答案
相关题目
印刷一张矩形的张贴广告（如图），它的印刷面积是32dm2，上下空白各1dm，两边空白各0.5dm．当要求四周空白处的面积为18dm2时，求用来印刷这张广告的纸张的长和宽各是多少（图中长度的单位：dm）．
如图，△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA相邻的外角平分线CF于点F，点O运动到何处时，四边形AECF是矩形？
12、如图，在△ABC中，DE是AC的中垂线，AE=2.5cm，△ABD的周长是9cm，则△ABC的周长是
32、如图，粗线和细线是公交车从体育馆到少年宫的两条行驶路线．