题目内容
已知P是⊙O外一点，OP交⊙O于点A，PA=8，点P到⊙O的切线长为12，则⊙O的半径长为
5
5
．分析：连接圆心O和切点B，则得到直角△POB，设圆的半径是r，则OB=r，PA=PA+OA=8+r，在直角△POB中利用勾股定理即可得到一个关于r的方程，解方程即可求得r的值．
解答：
解：连接OB，
∵PB是圆的切线，
∴OB⊥PB．
设圆的半径是r，则OB=r，PA=PA+OA=8+r．
在直角△POB中，OP2=OB2+PB2，
则（8+x）2=x2+144，
解得：r=5．
故答案是：5．
解：连接OB，∵PB是圆的切线，
∴OB⊥PB．
设圆的半径是r，则OB=r，PA=PA+OA=8+r．
在直角△POB中，OP2=OB2+PB2，
则（8+x）2=x2+144，
解得：r=5．
故答案是：5．
点评：本题考查了切线的性质定理，运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2012•南京）如图，A、B是⊙O上的两个定点，P是⊙O上的动点（P不与A、B重合）、我们称∠APB是⊙O上关于点A、B的滑动角．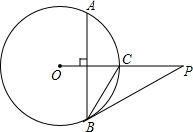
（2013•湖州）如图，已知P是⊙O外一点，PO交圆O于点C，OC=CP=2，弦AB⊥OC，劣弧AB的度数为120°，连接PB．
如图，已知A是⊙O外一点，B是⊙O上一点，AO的延长线交⊙O于C，连结BC．已知∠C=22.5°，∠BAC=45°，判断AB是否为⊙O的切线并说明理由．