��Ŀ����
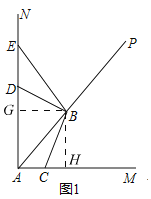
����Ŀ����֪��APƽ��![]() ����B������AP��һ���㣬��C��ֱ��AM���˶�������BC��
����B������AP��һ���㣬��C��ֱ��AM���˶�������BC��
![]() ��ͼ1��
��ͼ1��![]() ����
����![]() ����������BC��BA�ֱ��Ƶ�B˳ʱ����ת
����������BC��BA�ֱ��Ƶ�B˳ʱ����ת![]() ����ת��ǵ����߷ֱ�������AN���ڵ�D�͵�
����ת��ǵ����߷ֱ�������AN���ڵ�D�͵�![]() ����C������AM��ʱ����ֱ��д����
����C������AM��ʱ����ֱ��д����
![]() ��BC֮���������ϵ��______��
��BC֮���������ϵ��______��
![]() �߶�AC��AD��AB֮���������ϵ��______��
�߶�AC��AD��AB֮���������ϵ��______��
![]() ���
���![]() ����
����![]() ����������BC��BA�ֱ��Ƶ�B˳ʱ����ת
����������BC��BA�ֱ��Ƶ�B˳ʱ����ת![]() ����ת��ǵ����߷ֱ�������AN���ڵ�D�͵�E��
����ת��ǵ����߷ֱ�������AN���ڵ�D�͵�E��
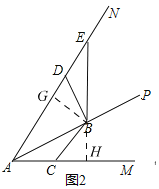
![]() ��ͼ2������C������AM��ʱ����̽���߶�AC��AD��AB֮���������ϵ��д�����۲�����֤����
��ͼ2������C������AM��ʱ����̽���߶�AC��AD��AB֮���������ϵ��д�����۲�����֤����
![]() ��ͼ3������C������AM�ķ����ӳ�����ʱ��BC������AN�ڵ�F����
��ͼ3������C������AM�ķ����ӳ�����ʱ��BC������AN�ڵ�F����![]() ��
��![]() ����ֱ��д���߶�AD��DF�ij���
����ֱ��д���߶�AD��DF�ij���

���𰸡�![]() ��
��![]() ��
��![]() ��
��![]() ��֤����������
��֤����������![]() ��
��![]() ��
��
��������
![]() ���жϳ�
���жϳ�![]() �������ó�
�������ó�![]() ���жϳ�
���жϳ�![]() ��
��![]() �����ɵó����ۣ�
�����ɵó����ۣ�
![]() ���жϳ��ı���AGBH�������Σ������ó�
���жϳ��ı���AGBH�������Σ������ó�![]() �����жϳ�
�����жϳ�![]() �����ɵó����ۣ�
�����ɵó����ۣ�
![]() ͬ
ͬ![]() �ķ������ɵó����ۣ�
�ķ������ɵó����ۣ�
![]() ��ͼ3�У���
��ͼ3�У���![]() ��G��
��G��![]() ��H��
��H��![]() ��
��![]() ��
��![]() ��֪��
��֪��![]() ��
��![]() ��
��![]() ��
��![]() ����֪
����֪![]() ��
��![]() ��
��![]() ���Ƴ�
���Ƴ�![]() ����
����![]() ���ɵ�
���ɵ�![]() ����
����![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ���ɵ�
���ɵ�![]() �����y���ɽ�����⣮
�����y���ɽ�����⣮
![]() ��ͼ1��
��ͼ1��
����B��![]() ��G��
��G��![]() ��H��
��H��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��ƽ���ߣ�
��ƽ���ߣ�![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
�ʴ�Ϊ![]() ��
��
![]() ��ͼ1����
��ͼ1����![]() ֪������B��
֪������B��![]() ��G��
��G��![]() ��H��
��H��
![]() ��
��
![]() �ı���AGBH�Ǿ��Σ�
�ı���AGBH�Ǿ��Σ�
��![]() ֪��
֪��![]() ��
��
![]() ����AGBH��������
����AGBH��������
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
�ʴ�Ϊ��![]() ��
��
![]() ��ͼ2��
��ͼ2��
����B��![]() ��G��
��G��![]() ��H��
��H��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��ƽ���ߣ�
��ƽ���ߣ�![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��ƽ���ߣ�
��ƽ���ߣ�
![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��
![]() ��ͼ3�У�
��ͼ3�У�
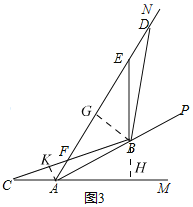
��![]() ��G��
��G��![]() ��H��
��H��![]() ��K��
��K��
��![]() ��֪��
��֪��![]() ��
��![]() ��
��
��֤��![]() ��
��![]() ��
��
��֪![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
��![]() ����
����![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
����ƽ���������ã�![]() ��
��
���![]() ��
��![]() ����AC����ȥ
����AC����ȥ![]()
![]() ��
��
����![]() ��
��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�