题目内容
如图所示，B、C是线段AD上任意两点，M是AB的中点，N是CD中点，若MN=16，BC=5，则线段AD的长是________．
27
分析：由已知条件可知，MN=MB+CN+BC，又因为M是AB的中点，N是CD中点，则AB+CD=2（MB+CN），故AD=AB+CD+BC可求．
解答：∵MN=MB+CN+BC=16，BC=5
∴MB+CN=11
∵M是AB的中点，N是CD中点
∴AB+CD=2（MB+CN）=22
∴AD=22+5=27
∴线段AD的长是27．
点评：利用中点性质转化线段之间的倍分关系是解题的关键，在不同的情况下灵活选用它的不同表示方法．
分析：由已知条件可知，MN=MB+CN+BC，又因为M是AB的中点，N是CD中点，则AB+CD=2（MB+CN），故AD=AB+CD+BC可求．
解答：∵MN=MB+CN+BC=16，BC=5
∴MB+CN=11
∵M是AB的中点，N是CD中点
∴AB+CD=2（MB+CN）=22
∴AD=22+5=27
∴线段AD的长是27．
点评：利用中点性质转化线段之间的倍分关系是解题的关键，在不同的情况下灵活选用它的不同表示方法．
练习册系列答案
相关题目
如图所示，A、B是4×5网格中的格点（网格线的交点），网格中的每个小正方形的边长都是1．
23、如图所示，已知O是∠EPF的平分线上的一点，以O为圆心的圆与角的两边分别交于点A、B和C、D．
如图所示，已知AD是∠EAC的平分线，且AD∥BC，求证：∠B=∠C．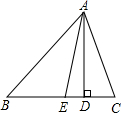
如图所示，AD，AE是三角形ABC的高和角平分线，∠B=36°，∠C=76°，求∠DAE的度数．