题目内容
正方形网格中，∠AOB如图放置，则sin∠AOB=（ ）A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
分析：找出以∠AOB为内角的直角三角形，根据正弦函数的定义，即直角三角形中∠AOB的对边与斜边的比，就可以求出．
解答：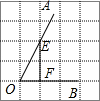
解：如图，作EF⊥OB，则EF=2，OF=1，由勾股定理得，OE=
，
∴sin∠AOB=
=
=
．
故选B．
解：如图，作EF⊥OB，则EF=2，OF=1，由勾股定理得，OE=| 5 |
∴sin∠AOB=
| EF |
| OE |
| 2 | ||
|
2
| ||
| 5 |
故选B．
点评：通过构造直角三角形来求解，利用了锐角三角函数的定义．
练习册系列答案
相关题目
动手操作：如图，在10×10的正方形网格中，有一矩形ABCD．
动手操作：如图，在10×10的正方形网格中，有一矩形ABCD．
．
的三个顶点
、
、
都在格点上．
（1）画出
后得到的三角形；（2）求AO在上述旋转过程中所扫过的面积．
．