题目内容
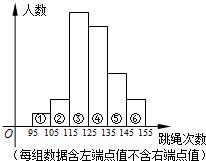
30、为了解某校学生的体能情况，随机抽取了该校部分学生进行引体向上测试，并将所得数据整理后绘制成频率分布直方图（如图所示）．已知图中从左到右前三个小组的频率分别为0.1、0.3、0.4，最左边小组的频数为5．根据图示提供的信息填空：（1）最右边的一个小组的频率是
0.2
．（2）参加这次测试的学生人数是
50
．（3）这次测试成绩的中位数在从左数起的第
3
小组内．（4）假设次数在8次或8次以上为达标，由此可估计该校学生测试的达标率为
60%
．分析：（1）由频率和为1可求出最右边的一个小组的频率；
（2）由$frac{频数}{总数}$=频率可得到参加这次测试的学生人数；
（3）根据中位数定义将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数，偶数个时求中间两个数的平均数可得答案．
（4）用达标人数÷总数×100%=达标率．
（2）由$frac{频数}{总数}$=频率可得到参加这次测试的学生人数；
（3）根据中位数定义将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数，偶数个时求中间两个数的平均数可得答案．
（4）用达标人数÷总数×100%=达标率．
解答：解：（1）1-0.1-0.3-0.4=0.2；
（2）5÷0.1=50；
（3）第一小组人数：5，
第二小组的人数：50×0.3=15，
第三小组的人数：50×0.4=20，
第四小组的人数：50×0.2=10，
位置处于中间的是第25各和26个，在第3小组；
（4）（20+10）÷50×100%=60%．
故答案为：0.2，50，3，60%．
（2）5÷0.1=50；
（3）第一小组人数：5，
第二小组的人数：50×0.3=15，
第三小组的人数：50×0.4=20，
第四小组的人数：50×0.2=10，
位置处于中间的是第25各和26个，在第3小组；
（4）（20+10）÷50×100%=60%．
故答案为：0.2，50，3，60%．
点评：此题主要考查了对频率、频数灵活运用的综合考查，各小组频数之和等于数据总和，各小组频率之和等于1，这是中考中的热点．
练习册系列答案
相关题目
测试，并指定甲、乙、丙、丁四名同学对这次测试结果的数据作出整理，下图是这四名同学提供的部分信息：
为了解某校学生的体能情况，随机抽取了该校部分学生进行引体向上测试，并将所得数据整理后绘制成频率分布直方图（如图所示）．已知图中从左到右前三个小组的频率分别为0.1、0.3、0.4，最左边小组的频数为5．根据图示提供的信息填空：
