Question

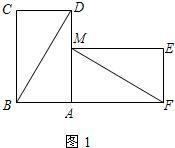
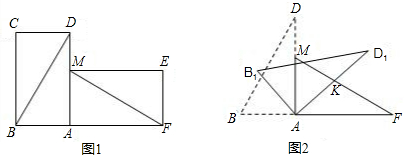
有两张完全重合的三角形纸片，小亮同学将其中一张绕点A顺时针旋转90°后得到三角形AMF（如图1），若此时他测得BD=8cm，
∠ADB=30°．
（1）试探究线段BD与线段MF的数量关系，并简要说明理由；
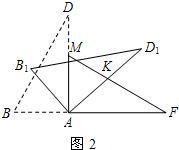
（2）小红与小亮同学继续探究．他们将△ABD绕点A顺时针旋转得△AB₁D₁，AD₁交FM于点K（如图2），设旋转角为β（0°＜β＜
90°），当△AFK为等腰三角形时，求旋转角β的度数；
（3）在图2基础上小强同学继续探究，过点K作KC∥B₁D₁交AB₁于点C，连接CM，（如图3）求证：△ACM∽△AKF；
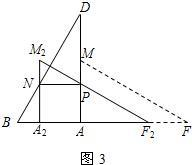
（4）若将△AFM沿AB方向平移得到△A₂F₂M₂（如图4），F₂M₂与AD交于点P，A₂M₂与BD交于点N，当NP∥AB时，求平移的距离是多少？

Answer 1

【答案】分析：（1）由旋转的性质可以证明△BAD≌△MAF．就可以得出线段BD=MF的数量关系．
（2）由条件可知∠F=30°，当∠F为顶角时，可以求出∠KAF=75°，从而求出旋转角β的度数，当∠F为底角时，可以求出∠KAF=30°，从而求出旋转角β的度数．
（3）由条件可以证明△ACK∽△AB₁D₁，可以得出=，由AB₁=AM，AF=AD₁可以得到=．再由∠B₁AM=∠D₁AF，就可以得出△ACM∽△AKF．从而得出结论．
（4）由题意知四边形PNA₂A为矩形，设A₂A=x，则PN=x．由条件根据勾股定理可以求出AF₂的值，AP的值，再可以得到△DNP∽△DBA，利用相似三角形的性质就可以求出A₂A的值．
解答：（1）线段BD与MF的数量关系是：BD=MF．
证明：∵△MAF是由△BAD旋转得来的，
∴△BAD≌△MAF．
∴BD=MF．
∴BD与MF的数量关系是：BD=MF．

（2）解：当∠F为顶角时，
∴∠AKF=∠KAF，
∴∠AKF+∠KAF+∠F=180°，且∠F=30°．
∴∠KAF==75°．
∴∠MAK=15°．
即β=15°．
当∠F为底角时，
∠F=∠KAF，
∵∠F=30°．
∴∠KAF=30°．
∴∠MAK=60°，即β=60°．
综上所述：当∠F为顶角时，β=15°．
当∠F为底角时，β=60°．

（3）证明：∵KC∥B₁D₁，
∴△ACK∽△AB₁D₁．
∴=．
∵△AB₁D₁≌△AMF，
∴AB₁=AM，AF=AD₁，
∴=．
∵∠B₁AD₁=∠MAF=90°，
∴∠B₁AM=∠D₁AF，
∴△ACM∽△AKF．

（4）解：如图4，由题意知四边形PNA₂A为矩形，设A₂A=x，则PN=x．
在Rt△A₂M₂F₂中，
∵M₂F₂=MF=BD=8，∠A₂F₂M₂=∠AFM=∠ADB=30°．
∴M₂A₂=4，A₂F₂=，
∴AF₂=-x．
在Rt△PAF₂中，
∵∠PF₂A=30°．
∴AP=AF₂•tan30°=（-x）•=4-x．
∴PD=AD-AP=-4+x．
∵NP∥AB，
∴∠DNP=∠B．
∵∠D=∠D，
∴△DNP∽△DBA．
∴=
∴=，
解得x=6-．
即A₂A=6-．
故平移的距离是（6-）cm．
点评：本题是一道综合性比较强的几何综合试题．考查了旋转的性质，相似三角形的判定与性质，勾股定理的运用，等腰三角形的性质的运用．在利用相似三角形的性质时注意使用相等线段的代换．