Question

【题目】如图，AB为半圆O的直径，C是半圆上一点，且∠BOC＝60°，设弓形AmC，△AOC，扇形BOC的面积分别为S1，S2，S3，则它们之间的大小关系是（　　）

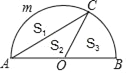
A. S1＜S2＜S3 B. S2＜S1＜S3 C. S2＜S3＜S1 D. S3＜S2＜S1

Answer 1

【答案】C

【解析】

设出圆的半径，利用扇形的面积公式表示出S3和S1+S2，利用锐角三角函数表示出CD，进而表示出S2，用作差表示出S1，即可得出结论．

解：设半圆⊙O的半径为r，则OA＝OB＝OC＝r，

∵∠BOC＝60°，

∴S3＝≈0.523r2，S1+S2＝＝πr2

如图，过点C作CD⊥AB于D，

在Rt△ODC中，∠BOC＝60°，

∴CD＝OCsin∠BOC＝r×sin60°＝r，

∴S2＝OA×CD＝r×r＝r2≈0.433r2，

∴S1＝S1+S2﹣S2＝πr2﹣r2＝（π﹣）r2≈0.613r2，

∵0.433r2＜0.523r2＜0.613r2，

∴S2＜S3＜S1，

故选：C．