Question

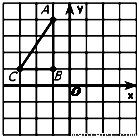
（10分）右图是反映今年泰州市溱湖风景区划船比赛中，甲、乙两船在比赛时，路程y（千米）

与时间x（小时）函数图象，请根据图象所提供的信息解答下列问题：

（1）先到达终点的是 船；该船的速度是每小时 千米；

（2）在哪一段时间，甲船的速度大于乙船的速度？

（3）点P是两条线的一个交点，它表示 ；你能求出该点所对应的时间吗？

Answer 1

（1）乙 16 （2）0＜x＜1 （3）甲乙两船相遇

【解析】

试题分析：（1）根据图象可得乙船先到达终点，它的速度一直是；（2）分别求出甲船在OQ和QB两段的速度与乙船的速度比较大小即可；（3）点P表示甲乙两船相遇，分别求出直线OA和QB的解析式，然后求出它们的交点坐标即可.

试题解析：（1）根据图象可得乙船先到达终点，它的速度一直是；（2）甲船在OQ段的速度=， 甲船在QB两段的速度=，所以甲船在OQ段的速度大于乙船的速度，所以0＜x＜1；（3）点P表示甲乙两船相遇，设直线OA的解析式为y=kx，把（1,16）代入得16=k，所以y=16x，设直线QB的解析式为y=mx+n，把（1,20）（2.5,35）代入得，解得，所以y=10x+10，，解得，所以两船在出发后小时时相遇.

考点：1.函数的图象；2.待定系数法求函数解析式；3.一次函数的实际应用.