题目内容
若关于x、y的二元一次方程组
的解满足不等式x＜0，y＞0，求k的取值范围．
解：
，
①-②得：3y=k+7，
y=
；
②×2+①得：x=
，
∵x＜0，y＞0，
∴
，
解得：-7＜k＜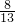
．
分析：首先用①-②，用含k的代数式表示y，再用②×2+①，用含k的代数式表示x，然后再根据x＜0，y＞0可得关于k的不等式组，再解不等式组即可．
点评：此题主要考查了解一元一次不等式组，以及二元一次方程组的解，关键是正确用含k的代数式表示y、x．
，①-②得：3y=k+7，
y=
；②×2+①得：x=
，∵x＜0，y＞0，
∴
，解得：-7＜k＜
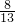．分析：首先用①-②，用含k的代数式表示y，再用②×2+①，用含k的代数式表示x，然后再根据x＜0，y＞0可得关于k的不等式组，再解不等式组即可．
点评：此题主要考查了解一元一次不等式组，以及二元一次方程组的解，关键是正确用含k的代数式表示y、x．
练习册系列答案
津桥教育计算小状元系列答案
相关题目