Question

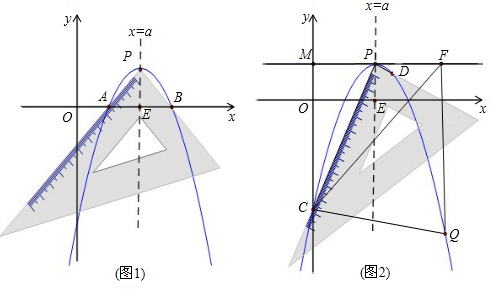
把一块三角板置于平面直角坐标系中，三角板的直角顶点为，两直角边与轴交于、，如图1，测得，.以为顶点的抛物线恰好经过、两点,抛物线的对称轴与轴交于点.

(1) 填空:     ,      ,点的坐标为       ；

(2)设抛物线与轴交于点，过作直线⊥轴,垂足为.如图2,把三角板绕着点旋转一定角度，使其中一条直角边恰好过点，另一条直角边与抛物线的交点为，试问：点、、三点是否在同一直线上？请说明理由.

(3)在（2）的条件下，若为抛物线上的一动点, 连结、，过作⊥,垂足为.试探索：是否存在点，使得是以为腰的等腰三角形？若存在，请求出的值；若不存在，请说明理由．

 

Answer 1

【答案】

（1），，（2）点、、三点在同一直线上，理由见解析，(3) 当，4或时，是以为腰的等腰三角形.

【解析】解：（1），，………………（3分）

（2）过作⊥于点，

则有，

由题意可知，，即

∵⊥轴

∴

∴

∴∽，所以………（4分）

(注：本式也可由得到)

设点坐标为，则，，又，，

∴解得，（不合舍去）.

∴点坐标为    …………………（6分）

又设直线的解析式为,由题意得

解得

∴直线的解析式为

,    …………………（7分）

当时,

∴点在直线上,即点、、三点在同一直线上. ……………（8分）

（３）存在.

由勾股定理可得：

,  , ……………（9分）

当时，有

 ∴　　解得

又∵在抛物线上，

∴　

∴解得,      …………………（11分）

当时，有，

∴　　解得，（不合题意舍去）

由解得：，

综上所述，当，4或时，是以为腰的等腰三角形. ……………（13分）

（1）根据二次函数图象的对称性以及等腰直角三角形的性质求出点A的坐标，然后代入函数解析式，计算即可求得值；

（2）过作⊥于点，证得∽，得出，设点坐标为，代入求得点坐标，求得直线的解析式，把代入的解析式，得出结论

（３）由勾股定理可得：,  ,，分两种情况讨论，①当时，②当时，求出的值