题目内容
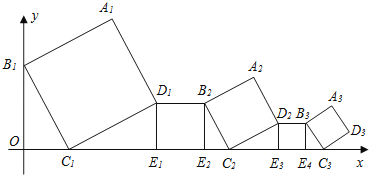
【题目】图
为奇数排成的数表，用十字框任意框出
个数，记框内中间这个数为
，其它四个数分别记为
，
，
，
（如图
）；图
为按某一规律排成的另一个数表，用十字框任意框出个数，记框内中间这个数为
，其它四个数记为
，
，
，
（如图
）．
（1）请你含的代数式表示．
（2）请你含的代数式表示．
（3）若
，
，求
的值．
【答案】（1）b=m－18；（2）
；（3）
【解析】
（1）根据图1可知：十字框中上方的数比中间的数大18，即可得出结论；
（2）根据图2可知：当中间数为正数时，十字框中左侧的数与中间的数的和为2；当中间数为负数时，十字框中左侧的数与中间的数的和为-2，即可得出结论；
（3）根据图1找到a、b、c、d与m的关系，即可求出k的值；然后对n进行分类讨论：当n＞0时，找出
，
，
，
与n的关系即可求出p的值，代入求值即可；当n＜0时，找出，，，与n的关系即可求出p的值，代入求值即可
解：（1）根据图1可知：十字框中上方的数比中间的数大18，
即b=m－18；
（2）根据图2可知：当n＞0时，n＋e=2
解得：e=2－n；
当n＜0时，n＋e=-2
解得：e=-2－n；
综上所述：
（3）根据图1可知：a=m－2，b= m－18，c= m＋2，d= m＋18
∵
∴k=4
根据图1可知：当n＞0时，n+f=18，n+e=2，n+g=-2，n+h=-18
∴f=18-n，e=2-n，g=-2-n，h=-18-n
∴
∴p=-4
∴此时
=4＋3×（-4）=-8；
当n＜0时，n+f=-18，n+e=-2，n+g=2，n+h=18
∴f=-18-n，e=-2-n，g=2-n，h=18-n
∴
∴p=-4
∴此时=4＋3×（-4）=-8；
综上所述：．
阅读快车系列答案【题目】某校八年级两个班，各选派10名学生参加学校举行的“建模”大赛预赛，各参赛选手的成绩如下：
八（1）班：88，91，92，93，93，93，94，98，98，100；
八（2）班：89，93，93，93，95，96，96，98，98，99.
通过整理，得到数据分析表如下：
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
八（1）班 | 100 |
| 93 | 93 | 12 |
八（2）班 | 99 | 95 |
|
| 8.4 |
（1）直接写出表中
、
、
的值为：
_____，
_____，
_____；
（2）依据数据分析表，有人说：“最高分在（1）班，（1）班的成绩比（2）班好.”但也有人说（2）班的成绩要好.请给出两条支持八（2）班成绩好的理由；
（3）学校从平均数、中位数、众数、方差中选取确定了一个成绩，等于或大于这个成绩的学生被评定为“优秀”等级，如果八（2）班有一半的学生能够达到“优秀”等级，认为这个成绩应定为_____分.
