题目内容
小明同学骑自行车去郊外春游,图中表示的是他离家的距离y(千米)与所用的时间(小时)之间关系的函数图象.
(1)根据图象回答:小明到达离家最远的地方需几小时?此时离家多远?
(2![]() )求小明出发两个半小时离家多远?
)求小明出发两个半小时离家多远?
(3)求小明出发多长时间距家12千米?

分析:(1)根据分段函数图象上点的坐标的意义可知:小明到达离家最远的地方需3小时,此时,他离家30千米;
(2)因为C(2,15)、D(3,30)在直线上,利用待定系数法求出解析式后,把=2.5代入解析式即可;
(3)分别利用待定系数法求得过E、F两点所在直线解![]() 析式以及过A、B两点所在直线解析式,分别令y=12,求出.
析式以及过A、B两点所在直线解析式,分别令y=12,求出.
解:(1)由图象可知小明到达离家最远的地方需3小时.此时,他离家30千米.
(2)设CD的解析式为y=k1+b1,将C(2,15)、D(3,30),
代入得解得
∴ =15-15(2≤≤3).
当=2.5时,y=22.5.
答:出发两个半小时,小明离家22.5千米.
(3)设过E、F两点的直线解析式为y=k2+b2,
将E(4,30),F(6,0),代入得解得
∴ =-15+90.(当
设过A、B两点的直线解析式为y=k3,
∵ B(1,15),∴ ∴ y=15.
当y=12时,=![]() .
.
答:小明出发![]() 小时和
小时和![]() 小时时距家12千米.
小时时距家12千米.

练习册系列答案
相关题目
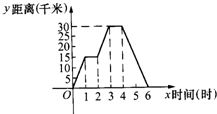 17、小明同学骑自行车去郊外春游,如图表示他离家的距离y(千米)与所用时间x(时)之间关系的函数图象,请根据图象回答:小明到达离家最远的地方用了
17、小明同学骑自行车去郊外春游,如图表示他离家的距离y(千米)与所用时间x(时)之间关系的函数图象,请根据图象回答:小明到达离家最远的地方用了
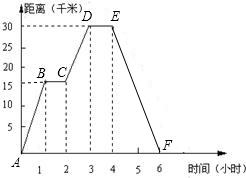 小明同学骑自行车去郊外春游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.
小明同学骑自行车去郊外春游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.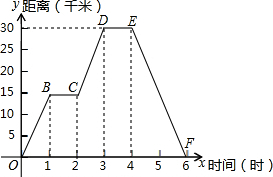 小明同学骑自行车去郊外秋游,如图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.
小明同学骑自行车去郊外秋游,如图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.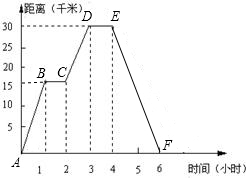 小明同学骑自行车去郊外春游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.
小明同学骑自行车去郊外春游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.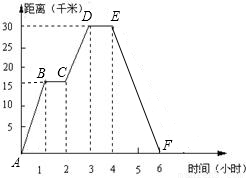 小明同学骑自行车去郊外春游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.
小明同学骑自行车去郊外春游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.