题目内容
如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).
(1)如果竖直摆放5个圆柱形桶时,网球能不能落入桶内?
(2)当竖直摆放圆柱形桶多少个时,网球可以落入桶内?
(1)不能
(2)当竖直摆放圆柱形桶8,9,10,11或12个时,网球可以落入桶内
解析:
解:(1)以点O为原点,AB所在直线为x轴建立直角坐标系(如图).……(1分)
M(0,5),B(2,0),C(1,0),D(,0)

设抛物线的解析式为,抛物线过点M和点B,则
,
.
即抛物线解析式为. ……(4分)
当x=时,y=;当x=
时,y=
.
即P(1,),Q(
,
)在抛物线上.
当竖直摆放5个圆柱形桶时,桶高=×5=
.
∵ <
且
<
,∴网球不能落入桶内. ……(5分)
(2)设竖直摆放圆柱形桶m个时网球可以落入桶内,
由题意,得,≤
m≤
. ……(6分)
解得,≤m≤
.
∵ m为整数,∴ m的值为8,9,10,11,12.
∴ 当竖直摆放圆柱形桶8,9,10,11或12个时,网球可以落入桶内.……(8分)

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
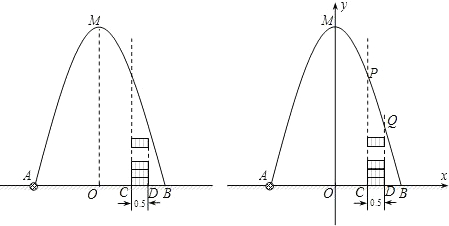
 飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).
飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计). 如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).以AB所在直线为x轴,OM所在直线为y轴建立平面直角坐标系.
如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).以AB所在直线为x轴,OM所在直线为y轴建立平面直角坐标系. 小红用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面点E处放一面平面镜,镜子与教学大楼的距离AE=20米.当她与镜子的距离CE=2.5米时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.6米,请你帮助小红测量出大楼AB的高度(注:入射角=反射角).
小红用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面点E处放一面平面镜,镜子与教学大楼的距离AE=20米.当她与镜子的距离CE=2.5米时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.6米,请你帮助小红测量出大楼AB的高度(注:入射角=反射角).