题目内容
 如图,已知P、O2是⊙O1上两点,⊙O1与⊙O2都经过A、B两点,PA的延长线和PB分别交于⊙O2于C、D两点.求证:
如图,已知P、O2是⊙O1上两点,⊙O1与⊙O2都经过A、B两点,PA的延长线和PB分别交于⊙O2于C、D两点.求证:(1)PO2平分∠APB;
(2)AC=BD.
考点:圆的综合题
专题:证明题
分析:(1)由圆的半径相等得出AO2=BO2,再由O2在⊙O1上,可得出
=
,由在同一个圆中等弧所对的圆周角相等得出∠APO2=∠BPO2,即可得出结论PO2平分∠APB.
(2)过O2分别做AC,BD的垂线交AC,BD于E,F,由角平分线的性质可得O2E=O2F,可证得△CO2E≌△BO2F,得出CE=BF,即可得出AC=BD.
 |
| AO2 |
 |
| BO2 |
(2)过O2分别做AC,BD的垂线交AC,BD于E,F,由角平分线的性质可得O2E=O2F,可证得△CO2E≌△BO2F,得出CE=BF,即可得出AC=BD.
解答:证明:(1)∵⊙O1与⊙O2都经过A、B两点,
∴AO2=BO2
∵O2在⊙O1上,
∴
=
,
∴∠APO2=∠BPO2
∴PO2平分∠APB
(2)如图,过O2分别做AC,BD的垂线交AC,BD于E,F
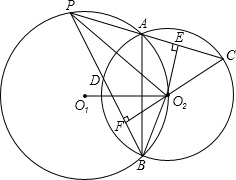
∵∠O2PE=∠O2PF,
∴O2E=O2F,
在△CO2E和△BO2F中,
,
∴△CO2E≌△BO2F(ASA),
∴CE=BF,
∵AC=2CE,BD=2BF,
∴AC=BD
∴AO2=BO2
∵O2在⊙O1上,
∴
 |
| AO2 |
 |
| BO2 |
∴∠APO2=∠BPO2
∴PO2平分∠APB
(2)如图,过O2分别做AC,BD的垂线交AC,BD于E,F

∵∠O2PE=∠O2PF,
∴O2E=O2F,
在△CO2E和△BO2F中,
|
∴△CO2E≌△BO2F(ASA),
∴CE=BF,
∵AC=2CE,BD=2BF,
∴AC=BD
点评:本题主要考查了圆的综合题,解题的关键利用角平分线的性质得出O2E=O2F.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
在-3,
,0,3四个数中,最小的数是( )
| 1 |
| 2 |
| A、-3 | ||
B、
| ||
| C、0 | ||
| D、3 |
设a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,d是倒数等于本身的有理数,则a-b+c2-|d|的值为( )
| A、0 | B、1 | C、0或1 | D、-1或1 |
 a,b,c三个数在数轴上的位置如图所示,则下列结论中错误的是( )
a,b,c三个数在数轴上的位置如图所示,则下列结论中错误的是( )| A、a+b<0 |
| B、a+c<0 |
| C、a-b>0 |
| D、b-c<0 |
 如图,MN为半圆O的直径,半径OA⊥MN,C为AM的中点,过点C作BC∥MN交⊙O于点B,求∠NBC的度数.
如图,MN为半圆O的直径,半径OA⊥MN,C为AM的中点,过点C作BC∥MN交⊙O于点B,求∠NBC的度数.