题目内容
阅读下面的材料:
如果关于x的方程ax2+bx+c=0(a≠0)有两个实数根x1,x2,则x1=
,x2=
,
∴x1+x2=
=-
,x1•x2=
=
=
;
综合得:若方程ax2+bx+c=0(a≠0)有两个实数根x1,x2,则有x1+x2=-
,x1•x2=
;
请利用这一结论解决问题:
(1)方程x2+bx+c=0的两根为-1和3,求b与c的值;
(2)设方程2x2-3x+1=0的两根为x1,x2,求
+
以及2x12+2x22的值.
如果关于x的方程ax2+bx+c=0(a≠0)有两个实数根x1,x2,则x1=
-b+
| ||
| 2a |
-b-
| ||
| 2a |
∴x1+x2=
| -2b |
| 2a |
| b |
| a |
| b2-(b2-4ac) |
| 4a2 |
| 4ac |
| 4a2 |
| c |
| a |
综合得:若方程ax2+bx+c=0(a≠0)有两个实数根x1,x2,则有x1+x2=-
| b |
| a |
| c |
| a |
请利用这一结论解决问题:
(1)方程x2+bx+c=0的两根为-1和3,求b与c的值;
(2)设方程2x2-3x+1=0的两根为x1,x2,求
| 1 |
| x1 |
| 1 |
| x2 |
(1)∵-1+3=-b,(-1)×3=c,
∴b=-2,c=-3;
(2)∵x1+x2=
,x1•x2=
,
∴
+
=
=
=3,
2x12+2x22=2(x12+x22)=2[(x1+x2)2-2x1x2]
=2[(
)2-2×
]=2(
-1)=
-2=
.
∴b=-2,c=-3;
(2)∵x1+x2=
| 3 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
| ||
|
2x12+2x22=2(x12+x22)=2[(x1+x2)2-2x1x2]
=2[(
| 3 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
| 9 |
| 2 |
| 5 |
| 2 |

练习册系列答案
相关题目
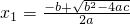 ,
,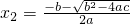 ,
,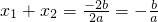 ,
, ;
;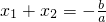 ,
,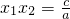 ;
; 以及2x12+2x22的值.
以及2x12+2x22的值. ,
, ,
, ,
, ;
; ,
,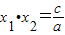 ;
; 以及2x12+2x22的值.
以及2x12+2x22的值. ,
, ,
, ,
, ;
; ,
, ;
; 以及2x12+2x22的值.
以及2x12+2x22的值.