题目内容
如图,已知AB是⊙O的直径,AB=8, 点C在半径OA上(点C与点O、A不重合),过点C作AB的垂线交⊙O于点D,连结OD,过点B作OD的平行线交⊙O于点E、交射线CD于点F.

(1)若 ,求∠F的度数;
(2)设 写出
写出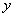 与
与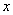 之间的函数解析式,并写出自变量取值范围;
之间的函数解析式,并写出自变量取值范围;
(3)设点C关于直线OD的对称点为P,若△PBE为等腰三角形,求OC的长.
(1)连结OE
∵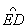 =
=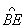 ∴∠BOE=∠EOD
∴∠BOE=∠EOD
∵OD//BF ∴∠DOE=∠BEO
∵OB=OE ∴∠OBE=∠OEB
∴∠OBE=∠OEB=∠BOE=60°
∵∠FCB=90°∴ ∠F=30°
(2)作OH⊥BE,垂足为H,
∵∠DCO=∠OHB=90°,OB=OD,∠O BE=∠COD
BE=∠COD
∴△HBO≌△COD
∴ 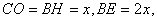
∵OD//BF ∴△COD∽△CBF ∴ 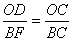
∴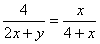 ∴
∴ 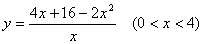
(3)∵∠COD=∠OBE,∠OBE=∠OEB,∠DOE=∠OEB
∴ ∠COD=∠DOE, ∴C关于直线OD的对称点为P在线段OE上
若△PBE为等腰三角形
① 当PB=PE,不合题意舍去;
② 当EB=EP 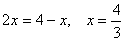
③ 当BE=BP 易证△OBE∽△BEP
∴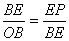 ∴
∴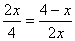
整理得: 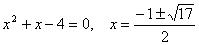 (负数舍去)
(负数舍去)
综上所述:当OC的长为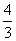 或
或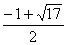 时,△PBE为等腰三角形。
时,△PBE为等腰三角形。

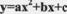 (a,b,c为常数,且
(a,b,c为常数,且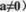 中的x与y的部分对应值如下表:
中的x与y的部分对应值如下表:
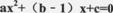 的
的 一个棉.(4)当x< -1或x>3时,
一个棉.(4)当x< -1或x>3时,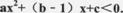 其中正确的个数为( )
其中正确的个数为( )
 = .
= . 是栏杆转动的支点,点
是栏杆转动的支点,点 是栏杆两段的连接点.当车辆经过时,栏杆
是栏杆两段的连接点.当车辆经过时,栏杆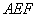 升起后的位置如图2所示,其示意图如图3所示,其中
升起后的位置如图2所示,其示意图如图3所示,其中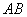 ⊥
⊥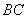 ,
, 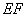 ∥
∥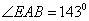 ,
,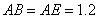 米,求当车辆经过时,栏杆EF段距离地面的高度(即直线EF上任意一点到直线BC的距离).(结果精确到0.1米,栏杆宽度忽略不计参考数据:sin 37° ≈ 0
米,求当车辆经过时,栏杆EF段距离地面的高度(即直线EF上任意一点到直线BC的距离).(结果精确到0.1米,栏杆宽度忽略不计参考数据:sin 37° ≈ 0 .60,cos 37° ≈ 0.80,tan 37° ≈ 0.75.)
.60,cos 37° ≈ 0.80,tan 37° ≈ 0.75.)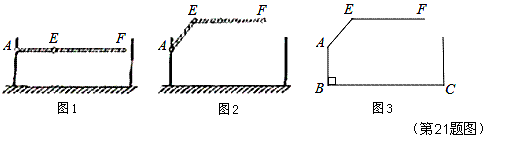
 纳米用科学记数法表示为 (
纳米用科学记数法表示为 (  ) (
) ( m (B)
m (B) m
m m
m  (D)
(D) m
m 
 ∠EFG=∠EGH=70°,∠BAC=∠ACD=∠EGF=∠EHG=50°,则下列叙述何者正确( )
∠EFG=∠EGH=70°,∠BAC=∠ACD=∠EGF=∠EHG=50°,则下列叙述何者正确( )