题目内容
在平面直角坐标系![]() 中,已知二次函数
中,已知二次函数![]() 的图象经过点
的图象经过点![]() 和点
和点![]() ,直线
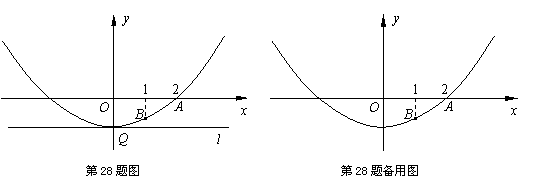
,直线![]() 经过抛物线的顶点且与
经过抛物线的顶点且与![]() 轴垂直,垂足为
轴垂直,垂足为![]() .
.
(1) 求该二次函数的表达式;
(2) 设抛物线上有一动点![]() 从点
从点![]() 处出发沿抛物线向上运动,其纵坐标
处出发沿抛物线向上运动,其纵坐标![]() 随时间
随时间
![]() ≥
≥![]() )的变化规律为
)的变化规律为![]() .现以线段
.现以线段![]() 为直径作
为直径作![]() .
.
①当点![]() 在起始位置点
在起始位置点![]() 处时,试判断直线
处时,试判断直线![]() 与
与![]() 的位置关系,并说明理由;在点
的位置关系,并说明理由;在点![]() 运动的过程中,直线
运动的过程中,直线![]() 与
与![]() 是否始终保持这种位置关系? 请说明你的理由;
是否始终保持这种位置关系? 请说明你的理由;
②若在点![]() 开始运动的同时,直线
开始运动的同时,直线![]() 也向上平行移动,且垂足
也向上平行移动,且垂足![]() 的纵坐标
的纵坐标![]() 随时间
随时间![]() 的变化规律为
的变化规律为![]() ,则当
,则当![]() 在什么范围内变化时,直线
在什么范围内变化时,直线![]() 与
与![]() 相交? 此时,若直线
相交? 此时,若直线![]() 被
被![]() 所截得的弦长为
所截得的弦长为![]() ,试求
,试求![]() 的最大值.
的最大值.
 |
解:(1)将点![]() 和点
和点![]() 的坐标代入,得
的坐标代入,得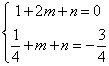 ,解得
,解得![]() ,
,
∴二次函数的表达式为![]() ……………………………………………………3分
……………………………………………………3分
(2)①当点![]() 在点
在点![]() 处时,直线
处时,直线![]() 与
与![]() 相切,理由如下:
相切,理由如下:
∵点![]() ,∴圆心的坐标为
,∴圆心的坐标为![]() ,∴
,∴![]() 的半径为
的半径为![]() ,
,
又抛物线的顶点坐标为(0,-1),即直线l上所有点的纵坐标均为-1,从而圆心C到直线l的距离为![]() ,∴直线
,∴直线![]() 与
与![]() 相切. …………………… 5分
相切. …………………… 5分
在点![]() 运动的过程中,直线
运动的过程中,直线![]() 与
与![]() 始终保持相切的位置关系,理由如下:
始终保持相切的位置关系,理由如下:
方法一: 设点![]() ,则圆心的坐标为
,则圆心的坐标为![]() ,∴圆心C到直线l的距离为
,∴圆心C到直线l的距离为![]() ,又∵
,又∵![]() ,∴
,∴![]() ,则
,则![]() 的半径为
的半径为![]() ,
,
∴直线![]() 与
与![]() 始终相切. ………………………………………………………… 7分
始终相切. ………………………………………………………… 7分
方法二: 设点![]() ≥1),则圆心的坐标为
≥1),则圆心的坐标为![]() ,∴
,∴![]() 的半径为
的半径为![]() ,而圆心C到直线l的距离为
,而圆心C到直线l的距离为![]() ,∴直线
,∴直线![]() 与
与![]() 始终相切.…………………… 7分
始终相切.…………………… 7分
②由①知,圆C的半径为![]() .
.
又∵圆心C的纵坐标为![]() ,直线l上的点的纵坐标为
,直线l上的点的纵坐标为![]() ,所以
,所以
(ⅰ)当![]() ≥
≥![]() ,即
,即![]() ≤
≤![]() 时,圆心C到直线l的距离为
时,圆心C到直线l的距离为![]() ,则由
,则由![]() ,得
,得![]() ,解得
,解得![]() ,
,
∴此时![]() ≤
≤![]() ; ……………………………………………………………………8分
; ……………………………………………………………………8分
(ⅱ)当![]() <
<![]() ,即
,即![]() >
>![]() 时,圆心C到直线l的距离为
时,圆心C到直线l的距离为![]() ,则由
,则由![]() ,得
,得![]() ,解得
,解得![]() ,
,
∴此时![]() <
<![]() ;
;
综上所述,当![]() 时,直线
时,直线![]() 与
与![]() 相交. ………………………………………9分
相交. ………………………………………9分
(说明: 若学生就写成![]() ≤
≤![]() 或
或![]() <
<![]() ,得全分;若学生依据直观,只考虑圆心C在直线l下方的情况,解出
,得全分;若学生依据直观,只考虑圆心C在直线l下方的情况,解出![]() 后,就得
后,就得![]() ,也给全分)
,也给全分)
∵当![]() 时,圆心C到直线l的距离为
时,圆心C到直线l的距离为![]() ,又半径为
,又半径为![]() ,
,
∴![]() , ……………………11分
, ……………………11分
∴当![]() 时,
时, ![]() 取得最大值为
取得最大值为![]() .
.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB= 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.