题目内容
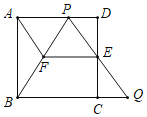
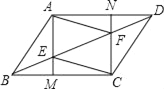
【题目】如图,反比例函数![]()
![]() 的图象经过点
的图象经过点![]() ,射线
,射线![]() 与反比例函数图象交于另一点
与反比例函数图象交于另一点![]() ;射线
;射线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,
,![]() 轴,垂足为
轴,垂足为![]() .
.

(1)求![]() 的值;
的值;
(2)求![]() 的值及直线
的值及直线![]() 的表达式;
的表达式;
【答案】(1)![]() ;(2)
;(2)![]() ;
;![]()
【解析】
(1)将点A的坐标代入解析式中易得k=2![]() ;
;
(2)过点![]() 做
做![]() 轴,垂足为
轴,垂足为![]() ,交
,交![]() 于F,根据反比例函数图象上点的坐标特征确定B点坐标为(1,2
于F,根据反比例函数图象上点的坐标特征确定B点坐标为(1,2![]() ),确定
),确定![]() ,可判断△ABF为等腰直角三角形,所以∠BAF=45°,得到∠DAC=∠BAC﹣∠BAF=30°,
,可判断△ABF为等腰直角三角形,所以∠BAF=45°,得到∠DAC=∠BAC﹣∠BAF=30°,![]() ,根据特殊角的三角函数值得
,根据特殊角的三角函数值得![]() ;由于AD⊥y轴,则OD=1,AD=2
;由于AD⊥y轴,则OD=1,AD=2![]() , 然后在Rt△OAD中利用正切的定义可计算出CD=2,易得C点坐标为(0,﹣1),于是可根据待定系数法求出直线AC的解析式为y=
, 然后在Rt△OAD中利用正切的定义可计算出CD=2,易得C点坐标为(0,﹣1),于是可根据待定系数法求出直线AC的解析式为y=![]() x﹣1.
x﹣1.
解:(1)![]() 反比例函数
反比例函数![]()
![]() 的图象经过点
的图象经过点![]() ,
,
![]() .
.
(2)如图,过点![]() 做
做![]() 轴,垂足为
轴,垂足为![]() ,交
,交![]() 于F.
于F.
![]() 点
点![]() 在反比例函数
在反比例函数![]() 的图象上.
的图象上.
![]() .
.
![]() .
.
![]() ,
,
![]() ∠BAC﹣∠BAF=30°,
∠BAC﹣∠BAF=30°,![]()
![]() ,
,
∵AD⊥y轴,点![]()
∴OD=1,AD=2![]() ,
,
![]() ,
,
∴![]() .
.
设直线![]() 的表达式为
的表达式为![]() ,
,
则有 ,
,
解得
![]() 直线
直线![]() 的表达式为
的表达式为![]()


练习册系列答案
相关题目