题目内容
如图,已知:反比例函数y= (m≠0)于一次函数y=kx+b(k≠0)的图象交于点A(4,1)和点
(m≠0)于一次函数y=kx+b(k≠0)的图象交于点A(4,1)和点 B(n,-4),直线AB与x轴、y轴分别交于点C、点D.
B(n,-4),直线AB与x轴、y轴分别交于点C、点D.
(1)求反比例函数和一次函数的解析式;
(2)求△COD的面积.
解:(1)∵反比例函数y= (m≠0)的图象过点A(4,1),
(m≠0)的图象过点A(4,1),
∴1= ,即m=4,
,即m=4,
∴反比例函数的解析式为:y= ;
;
∵比例函数y= 的图象过点B(n,4),
的图象过点B(n,4),
∴-4= ,解得n=-1,
,解得n=-1,
∴B(-1,-4),
∵一次函数y=kx+b(k≠0)的图象过点A(4,1)和点B(-1,-4),
∴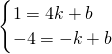 ,解得
,解得 ;
;
∴一次函数的解析式为:y=x-3;
(2)∵在一次函数y=x-3中,令x=0,则y=-3,
∴D(0,-3),即DO=3,
令y=0,则x=3,
∴C(3,0),即OC=3,
∴S△COD= OC•DO=
OC•DO= ×3×3=
×3×3= .
.
分析:(1)先把A点坐标代入反比例函数y= (m≠0)中求出m的值,进而可得出反比例函数的解析式,再把B点坐标代入即可求出n的值,把AB两点的坐标代入一次函数y=kx+b中接可求出k、b的值,进而可得出一次函数的解析式;
(m≠0)中求出m的值,进而可得出反比例函数的解析式,再把B点坐标代入即可求出n的值,把AB两点的坐标代入一次函数y=kx+b中接可求出k、b的值,进而可得出一次函数的解析式;
(2)由(1)中所求一次函数的解析式分别求出C、D两点坐标,利用三角形的面积公式即可进行解答.
点评:本题考查的是反比例函数与一次函数的交点问题及三角形的面积公式,熟知坐标轴上点的坐标特点是解答此题的关键.
 (m≠0)的图象过点A(4,1),
(m≠0)的图象过点A(4,1),∴1=
 ,即m=4,
,即m=4,∴反比例函数的解析式为:y=
 ;
;∵比例函数y=
 的图象过点B(n,4),
的图象过点B(n,4),∴-4=
 ,解得n=-1,
,解得n=-1,∴B(-1,-4),
∵一次函数y=kx+b(k≠0)的图象过点A(4,1)和点B(-1,-4),
∴
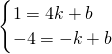 ,解得
,解得 ;
;∴一次函数的解析式为:y=x-3;
(2)∵在一次函数y=x-3中,令x=0,则y=-3,
∴D(0,-3),即DO=3,
令y=0,则x=3,
∴C(3,0),即OC=3,
∴S△COD=
 OC•DO=
OC•DO= ×3×3=
×3×3= .
.分析:(1)先把A点坐标代入反比例函数y=
 (m≠0)中求出m的值,进而可得出反比例函数的解析式,再把B点坐标代入即可求出n的值,把AB两点的坐标代入一次函数y=kx+b中接可求出k、b的值,进而可得出一次函数的解析式;
(m≠0)中求出m的值,进而可得出反比例函数的解析式,再把B点坐标代入即可求出n的值,把AB两点的坐标代入一次函数y=kx+b中接可求出k、b的值,进而可得出一次函数的解析式;(2)由(1)中所求一次函数的解析式分别求出C、D两点坐标,利用三角形的面积公式即可进行解答.
点评:本题考查的是反比例函数与一次函数的交点问题及三角形的面积公式,熟知坐标轴上点的坐标特点是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
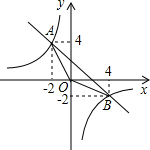 如图,已知一次函数y=kx+b的图象与反比例函数y=
如图,已知一次函数y=kx+b的图象与反比例函数y=| m |
| x |
| A、x<-2或0<x<4 |
| B、-2<x<4 |
| C、x>4或-2<x<0 |
| D、x<-2或x>4 |
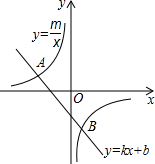 (2007•资阳)如图,已知点A(-4,2)、B( n,-4)是一次函数y=kx+b的图象与反比例函数
(2007•资阳)如图,已知点A(-4,2)、B( n,-4)是一次函数y=kx+b的图象与反比例函数 如图,已知反比例函数的图象经过点A,B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0)
如图,已知反比例函数的图象经过点A,B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0) 如图,已知反比例函数
如图,已知反比例函数 如图,已知一次函数y1=x+m(m为常数)的图象与反比例函数
如图,已知一次函数y1=x+m(m为常数)的图象与反比例函数