题目内容
8、若a+b<0,ab<0,则( )
分析:首先由ab<0,根据有理数的乘法法则,可知a,b异号,再由a+b<0,根据有理数的加法法则,又可推出负数的绝对值大于正数的绝对值.
解答:解:因为ab<0,所以a,b两数一正一负,
又a+b<0,所以负数的绝对值大于正数的绝对值.
故选D.
又a+b<0,所以负数的绝对值大于正数的绝对值.
故选D.
点评:本题考查了有理数的加法、乘法法则.绝对值不相等的异号两数相加,取绝对值较大的加数符号;两数相乘,异号得负.

练习册系列答案
相关题目
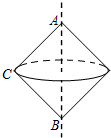 如图,Rt△ABC中,∠ACB=90°,AC=BC=2
如图,Rt△ABC中,∠ACB=90°,AC=BC=2| 2 |
| A、4π | ||
B、4
| ||
| C、8π | ||
D、8
|
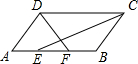 如图,?ABCD中,∠ADC与∠BCD的平分线分别交AB与F、E.
如图,?ABCD中,∠ADC与∠BCD的平分线分别交AB与F、E. 15、如图,若线段CD是由线段AB平移而得到的,则线段CD、AB关系是
15、如图,若线段CD是由线段AB平移而得到的,则线段CD、AB关系是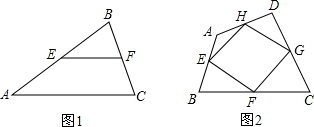
 如图,A、B两点分别位于一个池塘的两端,点C是AD的中点,也是BE的中点,若DE=20米,则AB=
如图,A、B两点分别位于一个池塘的两端,点C是AD的中点,也是BE的中点,若DE=20米,则AB=