题目内容
4.化简求值:$\frac{{x}^{2}+6x+9}{{x}^{2}-9}•\frac{x-3}{x+2}$=$\frac{1}{x+2}$,其中x2+2x=3.分析 原式第一项约分后,两项通分并利用同分母分式的减法法则计算得到最简结果,把已知等式代入计算即可求出值.
解答 解:原式=$\frac{(x+3)^{2}}{(x+3)(x-3)}$•$\frac{x-3}{x+2}$-$\frac{1}{x+2}$=$\frac{x+3}{x+2}$-$\frac{1}{x+2}$=$\frac{x+2}{x+2}$=1,
当x2+2x=3时,原式=1.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
15.某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
(1)这批样品的质量比标准质量多还是少?多或少几克?
(2)若标准质量为450克,则抽样检测的总质量是多少克?
| 与标准质量的差值/克 | -5 | -2 | 0 | 1 | 3 | 6 |
| 袋数 | 4 | 3 | 6 | 3 | 3 | 1 |
(2)若标准质量为450克,则抽样检测的总质量是多少克?
9.纳米是一种长度单位,已知某种植物花粉的直径约为35000纳米,那么用科学记数法表示该种花粉的直径为( )
| A. | 3.5×104米 | B. | 0.35×104米 | C. | 3.5×104纳米 | D. | 35×103纳米 |
13.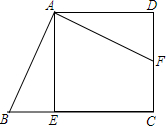 如图,在四边形ABCD中,AD∥BC,∠C=90°,点E,F分别在BC,CD上,若△ADF≌△AEB,则下列说法中不正确的是( )
如图,在四边形ABCD中,AD∥BC,∠C=90°,点E,F分别在BC,CD上,若△ADF≌△AEB,则下列说法中不正确的是( )
 如图,在四边形ABCD中,AD∥BC,∠C=90°,点E,F分别在BC,CD上,若△ADF≌△AEB,则下列说法中不正确的是( )
如图,在四边形ABCD中,AD∥BC,∠C=90°,点E,F分别在BC,CD上,若△ADF≌△AEB,则下列说法中不正确的是( )| A. | DF=EB | B. | AE⊥BC | C. | ∠DAF=∠EAB | D. | AB=AD |
