题目内容
 如图,△ABD、△AEC都是等边三角形,求证:BE=DC.
如图,△ABD、△AEC都是等边三角形,求证:BE=DC.
证明:∵△ABD、△AEC都是等边三角形,
∴AD=AB,AE=AC,∠DAB=∠CAE=60°,
∴∠DAC=∠BAC+60°,
∠BAE=∠BAC+60°,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
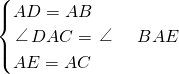 ,
,
∴△DAC≌△BAE(SAS),
∴BE=DC.
分析:利用△ABD、△AEC都是等边三角形,求证△DAC≌△BAE,然后即可得出BE=DC.
点评:此题考查学生对全等三角形的判定与性质和等边三角形的性质的理解与掌握,难度不大,是一道基础题.
∴AD=AB,AE=AC,∠DAB=∠CAE=60°,
∴∠DAC=∠BAC+60°,
∠BAE=∠BAC+60°,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
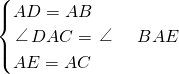 ,
,∴△DAC≌△BAE(SAS),
∴BE=DC.
分析:利用△ABD、△AEC都是等边三角形,求证△DAC≌△BAE,然后即可得出BE=DC.
点评:此题考查学生对全等三角形的判定与性质和等边三角形的性质的理解与掌握,难度不大,是一道基础题.

练习册系列答案
相关题目
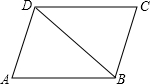 如图,△ABD≌△CDB,下面结论中不正确的是( )
如图,△ABD≌△CDB,下面结论中不正确的是( )| A、△ABD和△CDB的面积相等 | B、∠A+∠ABD=∠C+∠CBD | C、△ABD和△CDB的周长相等 | D、AD∥BC,且AD=BC |
 4、如图,∠ABD=90°,直线
4、如图,∠ABD=90°,直线 15、如图,∠ABD=∠CBD,DF∥AB,DE∥BC,则∠1与∠2的大小关系是
15、如图,∠ABD=∠CBD,DF∥AB,DE∥BC,则∠1与∠2的大小关系是 如图,△ABD中,点C、F分别为BD、AB上一点,AC、DF交于E,且CD=2BC,AE=2CE.求
如图,△ABD中,点C、F分别为BD、AB上一点,AC、DF交于E,且CD=2BC,AE=2CE.求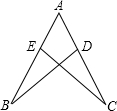 如图,△ABD≌△ACE,那么点B与点
如图,△ABD≌△ACE,那么点B与点