题目内容
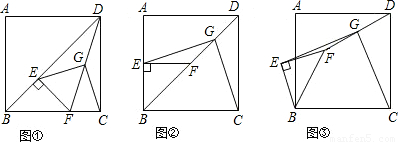
（2009•莱芜）将三角形纸片（△ABC）按如图所示的方式折叠，使点B落在变AC上，记为点B′，折痕为EF．已知AB=AC=3，BC=4，若FB′∥AB，那么BF的长度是| 12 |
| 7 |
| 12 |
| 7 |
分析：首先设BF=x，由折叠的性质可得：BF=BF′=x，又由AB=AC=3，BC=4，可得FC=4-x，然后由FB′∥AB，利用平行线分线段成比例定理，可得方程
=
，解此方程即可求得答案．
| x |
| 3 |
| 4-x |
| 4 |
解答：解：设BF=x，
由折叠的性质可得：BF=BF′=x，
∵FB′∥AB，
∴
=
，
∵AB=AC=3，BC=4，
∴FC=BC-BF=4-x，
∴
=
，
解得：x=
．
故答案为：
．
由折叠的性质可得：BF=BF′=x，
∵FB′∥AB，
∴
| B′F |
| AB |
| FC |
| BC |
∵AB=AC=3，BC=4，
∴FC=BC-BF=4-x，
∴
| x |
| 3 |
| 4-x |
| 4 |
解得：x=
| 12 |
| 7 |
故答案为：
| 12 |
| 7 |
点评：此题考查了折叠的性质与平行线分线段成比例定理．此题难度适中，注意掌握折叠前后图形的对应关系，注意数形结合思想与方程思想的应用．
练习册系列答案
相关题目
下滑动且始终保持和AB平行的伸缩横杆，△EMN是随MN滑动而变化的三角通风窗（阴影部分均不通风）．
