题目内容
【题目】如图,动点![]() 在双曲线
在双曲线![]() 上,动点
上,动点![]() 在双曲线
在双曲线![]() 上,且直线
上,且直线![]() 轴,若点
轴,若点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的横坐标为
的横坐标为![]() .
.
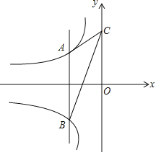
![]() 当
当![]() 取不同的值时,
取不同的值时,![]() 的面积________(填“变化”或者“不变化”);
的面积________(填“变化”或者“不变化”);
![]() 线段
线段![]() 的长可以用
的长可以用![]() 表示为________;
表示为________;
![]() 若点
若点![]() 的坐标为
的坐标为![]() ,请问是否存在常数
,请问是否存在常数![]() ,使得
,使得![]() 的面积等于
的面积等于![]() ?若有,请求出
?若有,请求出![]() 的值;若没有,请说明理由.
的值;若没有,请说明理由.
【答案】(1)不变化;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用t表示出A、B的纵坐标,则AB的长即可利用t表示出来,利用三角形的面积公式求解,即可判断;
(2)根据(1)的过程即可求解;
(3)分t>4和t<4两种情况进行求解,首先利用t表示出AB边上的高,根据三角形的面积公式列方程求解.
(1)当x=t时,A的纵坐标是:![]() ,B的纵坐标是:
,B的纵坐标是:![]() ,
,
则AB=![]()
![]() =
=![]() ,
,
则S△ABC=![]() AB(t)=
AB(t)=![]() ×(
×(![]() )×(t)=
)×(t)=![]() .
.
则当t取不同的值时,△ABC的面积不变化.
故答案为:不变化;
![]() 把
把![]() 代入
代入![]() ,得
,得![]() ,
,
把![]() 代入
代入![]() 得:
得:![]() .
.
线段![]() 的长可以用
的长可以用![]() 表示为:
表示为:![]() .
.
故答案是:![]() ;
;
![]() 当
当![]()
![]() 边上的高是:
边上的高是:![]() ,则
,则![]() ,
,
解得:![]() ;
;
当![]() 时,
时,![]() 边上的高是:
边上的高是:![]() ,则
,则![]() ,
,
解得:![]() .
.

练习册系列答案
相关题目