题目内容
已知实数a，b，c满足a≥b≥c，a+b+c=0且a≠0．设x1，x2是方程ax2+bx+c=0的两个实数根，则平面直线坐标系内两点A（x1，x2），B（x2，x1）之间的距离的最大值为________．
3
分析：首先利用两点之间的距离公式表示出|AB|的值，进而利用根与系数的关系以及a≥b≥c得出距离的最大值．
解答：|AB|=
，
=|x1-x2|，
=×
，
=×
，
=×
，
=×
，
=
，
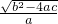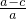∵a≥b≥c，
∴a≥-a-c≥c，
．
故答案为：3．
点评：此题主要考查了根与系数的关系以及两点之间的距离等知识，正确应用两点之间的距离公式是解决问题的关键．
分析：首先利用两点之间的距离公式表示出|AB|的值，进而利用根与系数的关系以及a≥b≥c得出距离的最大值．
解答：|AB|=
，=
|x1-x2|，=
×，=
×，=
×，=
×，=
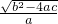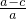，∵a≥b≥c，
∴a≥-a-c≥c，
．故答案为：3
．点评：此题主要考查了根与系数的关系以及两点之间的距离等知识，正确应用两点之间的距离公式是解决问题的关键．
练习册系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
（2013•菏泽）（1）已知m是方程x2-x-2=0的一个实数根，求代数式
有两个不相等的实数根x1,x2，求k的取值范围.
＞0
的值．
的图象交于A、B两点．
（1）已知m是方程x2-x-2=0的一个实数根，求代数式
的值．
的图象交于A、B两点．