题目内容
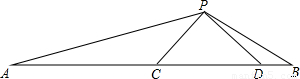
如图：△PCD是等腰直角三角形，∠DPC=90°，∠APB=135°
求证：（1）△PAC∽△BPD；
（2）若AC=3，BD=1，求CD的长．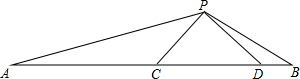
求证：（1）△PAC∽△BPD；
（2）若AC=3，BD=1，求CD的长．
证明：（1）∵△PCD是等腰直角三角形，∠DPC=90°，∠APB=135°，∴∠APC+∠BPD=45°，
又∠PAB+∠PBA=45°，∠PBA+∠PBD=45°，∴∠PAB=∠PBD，∠BPD=∠PAC，
∵∠PCA=∠PDB，∴△PAC∽△BPD；
（2）∵
=
，PC=PD，AC=3，BD=1
∴PC=PD=
，
∴CD=
=
．
又∠PAB+∠PBA=45°，∠PBA+∠PBD=45°，∴∠PAB=∠PBD，∠BPD=∠PAC，
∵∠PCA=∠PDB，∴△PAC∽△BPD；
（2）∵
| AC |
| PD |
| PC |
| BD |
∴PC=PD=
| 3 |
∴CD=
| 3+3 |
| 6 |
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
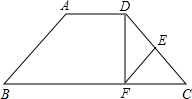如图，梯形ABCD中，AD∥BC，DE=EC，EF∥AB交BC于点F，EF=EC，连接DF．
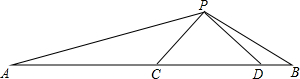如图：△PCD是等腰直角三角形，∠DPC=90°，∠APB=135°
如图：△PCD是等腰直角三角形，∠DPC=90°，∠APB=135°