题目内容
已知：如图，等腰直角三角形ABC的直角边长为16，D在AB上，且DB=4，M是在AC上的一动点，则DM+BM的最小值为（ ）分析：作点B，B′关于直线AC对称，连接DB′，DB′就是最短距离，利用勾股定理求得DB′的长度即可．
解答：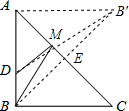
解：连接AB′，
∵△ABC是等腰直角三角形，
∴∠BAC=45°，
∵点B与点B′关于直线AC对称，
∴BE=B′E，∠AEB=∠AEB′，
在△ABE与△AB′E中，
∵
，
∴△ABE≌△AB′E，
∴△ABB′是等腰直角三角形，
∴AB′=AB=16，
∵AD=AB-DB=12，
DB′=
=
=20．
故选A．
解：连接AB′，∵△ABC是等腰直角三角形，
∴∠BAC=45°，
∵点B与点B′关于直线AC对称，
∴BE=B′E，∠AEB=∠AEB′，
在△ABE与△AB′E中，
∵
|
∴△ABE≌△AB′E，
∴△ABB′是等腰直角三角形，
∴AB′=AB=16，
∵AD=AB-DB=12，
DB′=
| AB′2+AD2 |
| 162+122 |
故选A．
点评：本题考查的是轴对称最短路线问题，根据题意作出辅助线，构造出直角三角形是，利用勾股定理求解是解答此题的关键．
练习册系列答案
相关题目
8、已知：如图，等腰直角三角形ABC中，∠ACB=90°，直线l经过点C，AD⊥l，BE⊥l，垂足分别为D，E．
相同．请你任选其中一个图形加以证明）
