题目内容
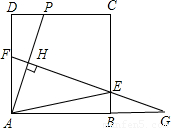
(2010•番禺区二模)如图,己知正方形ABCD的边长为12,点P为CD边上的一个动点(点P与D、C不重合),AP的垂直平分线EF分别交AD、AP、BC于点F、H、E,交AB的延长线于点G.(1)证明:△BGE∽△HAF;
(2)判断EF与AP是否相等,并给出证明;
(3)连AE,若△AEH的面积是△AFH面积的2倍,试求此时FG的长.
【答案】分析:(1)已知EF垂直平分AP可得∠AHF=∠GBE易证△BGE∽△HAF.
(2)做EM垂直AD,证明四边形EMDC为矩形,可得EM∥GA然后得证.
(3)本题要利用1,2问的答案利用三角函数进行解答.
解答: 证明:(1)在正方形ABCD中,AF∥BE,∠GBE=GAF=90°,
证明:(1)在正方形ABCD中,AF∥BE,∠GBE=GAF=90°,
∵AP的垂直平分线为EF,∴∠AHF=90°,
∴∠AHF=∠GBE,(1分)
又∵∠G+∠PAG=90°,∠HAF+∠PAG=90°,
∴∠G=∠HAF.(3分)
∴△BGE∽△HAF.(4分)
(2)EF=AP.(5分)
过E作EM⊥AD交AD于M,则四边形EMDC为矩形,
∴EM=CD=AD,(6分)
又∠EMD=90°,∠GAD=∠ADP=90°,
∴∠EMD=∠GAD=∠ADP,
∴GA∥EM.
∴∠FEM=∠G.(8分)
又由(1)△BGE∽△HAF,
∴∠FEM=∠G=∠DAP.(9分)
在△PDA和△FME中
∵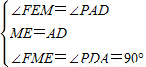 ,
,
∴△PDA≌△FME,∴EF=AP.(10分)
(3)由题意有: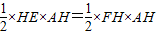 ,∴EH=2FH.(11分)
,∴EH=2FH.(11分)
∴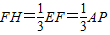 .∴
.∴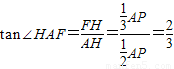 .
.
又在Rt△PDA和Rt△FHA中,
由tan∠HAF=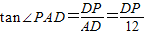 ,∴DP=8,(12分)
,∴DP=8,(12分)
∴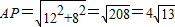 ,
,
∴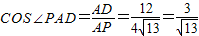 .同理
.同理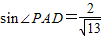 .
.
∴cos∠FAH=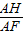 =
=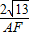 =
=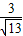 ,得AF=
,得AF=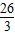 .(13分)
.(13分)
又在Rt△FAG中,
由 ,又sinG=sin∠PAD,
,又sinG=sin∠PAD,
∴sinG=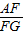 =
= =
=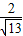 ,
,
得FG= .
.
即试求此时FG的长为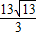 .(14分)
.(14分)
〖本题解法较多,如先求BG,HG等,其它解法可比照给分〗
点评:本题考查的是线段垂直平分线的性质(垂直平分线上任意一点,和线段两端点的距离相等)的有关知识以及矩形的判定定理.有一定难度.
(2)做EM垂直AD,证明四边形EMDC为矩形,可得EM∥GA然后得证.
(3)本题要利用1,2问的答案利用三角函数进行解答.
解答:
 证明:(1)在正方形ABCD中,AF∥BE,∠GBE=GAF=90°,
证明:(1)在正方形ABCD中,AF∥BE,∠GBE=GAF=90°,∵AP的垂直平分线为EF,∴∠AHF=90°,
∴∠AHF=∠GBE,(1分)
又∵∠G+∠PAG=90°,∠HAF+∠PAG=90°,
∴∠G=∠HAF.(3分)
∴△BGE∽△HAF.(4分)
(2)EF=AP.(5分)
过E作EM⊥AD交AD于M,则四边形EMDC为矩形,
∴EM=CD=AD,(6分)
又∠EMD=90°,∠GAD=∠ADP=90°,
∴∠EMD=∠GAD=∠ADP,
∴GA∥EM.
∴∠FEM=∠G.(8分)
又由(1)△BGE∽△HAF,
∴∠FEM=∠G=∠DAP.(9分)
在△PDA和△FME中
∵
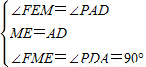 ,
,∴△PDA≌△FME,∴EF=AP.(10分)
(3)由题意有:
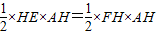 ,∴EH=2FH.(11分)
,∴EH=2FH.(11分)∴
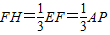 .∴
.∴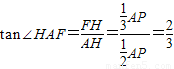 .
.又在Rt△PDA和Rt△FHA中,
由tan∠HAF=
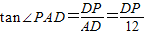 ,∴DP=8,(12分)
,∴DP=8,(12分)∴
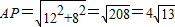 ,
,∴
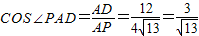 .同理
.同理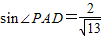 .
.∴cos∠FAH=
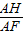 =
=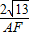 =
=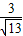 ,得AF=
,得AF=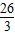 .(13分)
.(13分)又在Rt△FAG中,
由
 ,又sinG=sin∠PAD,
,又sinG=sin∠PAD,∴sinG=
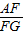 =
= =
=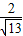 ,
,得FG=
 .
.即试求此时FG的长为
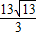 .(14分)
.(14分)〖本题解法较多,如先求BG,HG等,其它解法可比照给分〗
点评:本题考查的是线段垂直平分线的性质(垂直平分线上任意一点,和线段两端点的距离相等)的有关知识以及矩形的判定定理.有一定难度.

练习册系列答案
相关题目
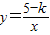 经过点C,试求实数k的值.
经过点C,试求实数k的值.