题目内容
 (2012•洪山区模拟)如图,在梯形ABCD中,AD∥BC,BC=DC,作CF平分∠BCD,DF∥AB,BF的延长线交DC于点E,求证:AD=DE.
(2012•洪山区模拟)如图,在梯形ABCD中,AD∥BC,BC=DC,作CF平分∠BCD,DF∥AB,BF的延长线交DC于点E,求证:AD=DE.分析:首先延长DF交BC于M,由AD∥BC,DF∥AB,可得四边形ABMD是平行四边形,即可证得AD=BM,然后证得△BCF≌△DCF(SAS),继而可证得△DEF≌△BMF(ASA),即可得DE=BM,继而证得AD=DE.
解答: 证明:延长DF交BC于M,
证明:延长DF交BC于M,
∵AD∥BC,DF∥AB,
∴四边形ABMD是平行四边形,
∴BM=AD,
∵CF平分∠BCD,
∴∠1=∠2,
在△BCF和△DCF中,
∵
,
∴△BCF≌△DCF(SAS),
∴∠3=∠4,BF=DF,
在△DEF和△BMF中,
∵
,
∴△DEF≌△BMF(ASA),
∴DE=BM,
∴AD=DE.
 证明:延长DF交BC于M,
证明:延长DF交BC于M,∵AD∥BC,DF∥AB,
∴四边形ABMD是平行四边形,
∴BM=AD,
∵CF平分∠BCD,
∴∠1=∠2,
在△BCF和△DCF中,
∵
|
∴△BCF≌△DCF(SAS),
∴∠3=∠4,BF=DF,
在△DEF和△BMF中,
∵
|
∴△DEF≌△BMF(ASA),
∴DE=BM,
∴AD=DE.
点评:此题考查了梯形的性质、平行四边形的判定与性质以及全等三角形的判定与性质.此题难度适中,解题的关键是准确作出辅助线,利用数形结合的思想求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
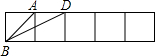 (2012•洪山区模拟)正方形网格中,△ABD如图放置,其顶点A、B、D都在格点上.
(2012•洪山区模拟)正方形网格中,△ABD如图放置,其顶点A、B、D都在格点上. (2012•洪山区模拟)如图,以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,过点D作切线DE交BC于E
(2012•洪山区模拟)如图,以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,过点D作切线DE交BC于E