题目内容
已知:二次函数y=x2-2(m-1)x+m2-2m-3,其中m为实数.
(1)求证:不论m取何实数,这个二次函数的图象与x轴必有两个交点;
(2)设这个二次函数的图象与x轴交于点A(x1,0)、B(x2,0),且x1、x2的倒数和为
,求这个二次函数的解析式.
(1)求证:不论m取何实数,这个二次函数的图象与x轴必有两个交点;
(2)设这个二次函数的图象与x轴交于点A(x1,0)、B(x2,0),且x1、x2的倒数和为
| 2 |
| 3 |
(1)∵△=b2-4ac=[-2(m-1)]2-4(m2-2m-3)=4m2-8m+4-4m2+8m+12=16>0,
∴不论m取何实数,这个二次函数的图象与x轴必有两个交点;
(2)∵x1+x2=2(m-1),x1x2=m2-2m-3,
+
=
,
即
=
,
=
,
解得m=0或5,
二次函数解析式为:y=x2+2x-3或y=x2-8x+12.
∴不论m取何实数,这个二次函数的图象与x轴必有两个交点;
(2)∵x1+x2=2(m-1),x1x2=m2-2m-3,
| 1 |
| x1 |
| 1 |
| x2 |
| 2 |
| 3 |
即
| x1+x2 |
| x1x2 |
| 2 |
| 3 |
| 2(m-1) |
| m2-2m-3 |
| 2 |
| 3 |
解得m=0或5,
二次函数解析式为:y=x2+2x-3或y=x2-8x+12.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知:二次函数的表达式为y=2x2+4x-1.
已知:二次函数的表达式为y=2x2+4x-1.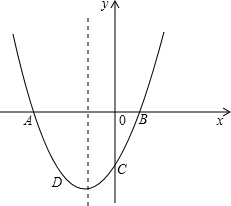 交于点C,点D(-2,-3)在抛物线上.
交于点C,点D(-2,-3)在抛物线上.