题目内容
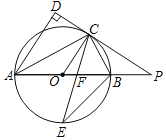
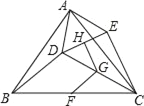
【题目】如图,△ABC为等腰三角形,AB=AC,D为△ABC内一点,连接AD,将线段AD绕点A旋转至AE,使得∠DAE=∠BAC,F,G,H分别为BC,CD,DE的中点,连接BD,CE,GF,GH.
(1)求证:GH=GF;
(2)试说明∠FGH与∠BAC互补.
【答案】(1)证明见解析;(2)说明见解析.
【解析】
(1)首先得出△ABD≌△ACE(SAS),进而利用三角形中位线定理得出GH=GF;
(2)利用全等三角形的性质结合平行线的性质得出∠FGH=∠DGF+∠HGD进而得出答案.
(1)∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中
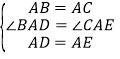 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∵F,G,H分别为BC,CD,DE的中点,
∴HG∥CE,GF∥BD,且GH=![]() CE,GF=
CE,GF=![]() BD,
BD,
∴GH=GF;
(2)∵△ABD≌△ACE,
∴∠ABD=∠ACE,
∵HG∥CE,GF∥BD,
∴∠HGD=∠ECD,∠GFC=∠DBC,
∴∠HGD=∠ACD+∠ECA=∠ACD+∠ABD,
∠DGF=∠GFC+∠GCF=∠DBC+∠GCF,
∴∠FGH=∠DGF+∠HGD
=∠DBC+∠GCF+∠ACD+∠ABD
=∠ABC+∠ACB
=180°﹣∠BAC,
∴∠FGH与∠BAC互补.

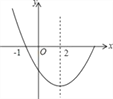
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他各项费用80元.
销售单价x(元) | 3.5 | 5.5 |
销售量y(袋) | 280 | 120 |
(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?