Question

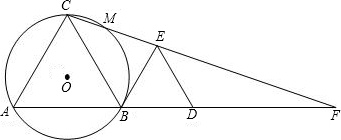
如图，B是线段AD上一点，△ABC和△BDE都是等边三角形，⊙O是△ABC的外接圆．CE与⊙O相交于G，CE的延长线与AD的延长线相交于F．
（1）求证：△BCF∽△DEF；
（2）求证：BE是⊙O的切线；
（3）若，求．

Answer 1

【答案】分析：（1）利用△ABC和△BDE都是等边三角形，得出BC∥DE，再利用∠BCF=∠DEF，∠F=∠F，得出△BCF∽△DEF；
（2）根据已知得出∠EBO=180°-（∠ABO+∠DBE）=90°，再利用切线的判定定理得出即可；
（3）根据BC∥DE得：，进而得出，，进而求出CE=3EG，从而．
解答：证明：（1）∵△ABC和△BDE都是等边三角形，
∴∠ABC=∠BDE=60°，
∴BC∥DE，
∴∠BCF=∠DEF，
又∵∠F=∠F，
∴△BCF∽△DEF；

（2）连接OB，∵⊙O是△ABC的外接圆，△ABC是等边三角形，
∴O也是△ABC的内心，
∴OB是∠ABC的平分线，∠ABO=∠ABC=30°，
∴∠EBO=180°-（∠ABO+∠DBE）=90°，
∴OB⊥BE，
∴BE是⊙O的切线；

（3）由（1）BC∥DE得：
，
所以DF=DB=DE，
所以∠F=∠DEF=∠BCE=30°，
连接OC、OG，与（2）同理得∠OCB=30°，
所以∠OCG=60°，
从而∠COG=60°，∠CBG=COG=30°，
在△EBC中，∠BCE=30°，∠CBE=60°，∠CEB=90°，
tan60°==，
所以，
同理在△EBG中，∠EBG=60°-30°=30°，∠GEB=90°，
tan30°=，
所以，
所以CE=3EG，
从而．
点评：此题主要考查了切线的判定与性质以及解直角三角形、相似三角形的判定，根据已知得出EG，CE与BE的关系是解题关键．