题目内容
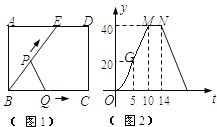
【题目】如图(1)所示，E为矩形ABCD的边AD上一点，动点P、Q同时从点B出发，点P以1cm/秒的速度沿折线BE—ED—DC运动到点C时停止，点Q以2cm/秒的速度沿BC运动到点C时停止．设P、Q同时出发t秒时，△BPQ的面积为ycm2．已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分，其余各部分均为线段)，则下列结论：
①当0＜t≤5时，y＝
t2；②当t＝6秒时，△ABE≌△PQB；③cos∠CBE＝
；
④当t＝
秒时，△ABE∽△QBP；
其中正确的是（ ）
A．①② B．①③④ C．③④ D．①②④
【答案】D
【解析】
试题分析：根据图（2）可以判断三角形的面积变化分为四段，①当点P在BE上运动，点Q到达点C时；②当点P到达点E时，点Q静止于点C，从而得到BC、BE的长度；③点P到达点D时，点Q静止于点C；④当点P在线段CD上，点Q仍然静止于点C时．
根据图（2）可得，当点P到达点E时点Q到达点C，
∵点P、Q的运动的速度分别是1cm/秒、2cm/秒
∴BC=BE=10，
∴AD=BC=10．
又∵从M到N的变化是4，
∴ED=4，
∴AE=AD-ED=10-4=6．
∵AD∥BC，
∴∠1=∠2，
故③错误；
如图1，过点P作PF⊥BC于点F，
∵AD∥BC，
∴∠1=∠2，
如图3，当t=6秒时，点P在BE上，点Q静止于点C处．
∴△ABE≌△PQB（SAS）．
故②正确；
又∵∠A=∠Q=90°，
∴△ABE∽△QBP，故④正确．
综上所述，正确的结论是①②④．
故选D．
练习册系列答案
小题狂做系列答案
相关题目
