题目内容
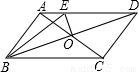
(2007•日照)如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于 .
【答案】分析:作B′F⊥AD,垂足为F,WE⊥B′F,垂足为E,根据绕顶点A逆时针旋转30°,计算出边,然后求面积.
解答: 解:如图,作B′F⊥AD,垂足为F,WE⊥B′F,垂足为E,
解:如图,作B′F⊥AD,垂足为F,WE⊥B′F,垂足为E,
∵四边形WEFD是矩形,∠BAB′=30°,
∴∠B′AF=60°,∠FB′A=30°,∠WB′E=60°,
∴B′F=AB′sin60°= ,AF=AB′cos60°=
,AF=AB′cos60°= ,WE=DF=AD-AF=
,WE=DF=AD-AF= ,
,
EB′=WE′cot60°= ,EF=B′F-B′E=
,EF=B′F-B′E= ,
,
∴S△B′FA= ,S△B′EW=
,S△B′EW= ,SWEFD=
,SWEFD= ,
,
∴公共部分的面积=S△B′FA+S△B′EW+SWEFD= ;
;
法2:连接AW,如图所示:

根据旋转的性质得:AD=AB′,∠DAB′=60°,
在Rt△ADW和Rt△AB′W中,
∵ ,
,
∴Rt△ADW≌Rt△AB′W(HL),
∴∠B′AW=∠DAW= DAB′=30°,
DAB′=30°,
又∵AD=AB′=1,
在Rt△ADW中,tan∠DAW= ,即tan30°=WD,
,即tan30°=WD,
解得:WD= ,
,
∴S△ADW=S△AB′W= WD•AD=
WD•AD= ,
,
则公共部分的面积=S△ADW+S△AB′W= .
.
故答案为 .
.
点评:本题利用了正方形的性质,三角形的面积公式,勾股定理求解.
解答:
 解:如图,作B′F⊥AD,垂足为F,WE⊥B′F,垂足为E,
解:如图,作B′F⊥AD,垂足为F,WE⊥B′F,垂足为E,∵四边形WEFD是矩形,∠BAB′=30°,
∴∠B′AF=60°,∠FB′A=30°,∠WB′E=60°,
∴B′F=AB′sin60°=
 ,AF=AB′cos60°=
,AF=AB′cos60°= ,WE=DF=AD-AF=
,WE=DF=AD-AF= ,
,EB′=WE′cot60°=
 ,EF=B′F-B′E=
,EF=B′F-B′E= ,
,∴S△B′FA=
 ,S△B′EW=
,S△B′EW= ,SWEFD=
,SWEFD= ,
,∴公共部分的面积=S△B′FA+S△B′EW+SWEFD=
 ;
;法2:连接AW,如图所示:

根据旋转的性质得:AD=AB′,∠DAB′=60°,
在Rt△ADW和Rt△AB′W中,
∵
 ,
,∴Rt△ADW≌Rt△AB′W(HL),
∴∠B′AW=∠DAW=
 DAB′=30°,
DAB′=30°,又∵AD=AB′=1,
在Rt△ADW中,tan∠DAW=
 ,即tan30°=WD,
,即tan30°=WD,解得:WD=
 ,
,∴S△ADW=S△AB′W=
 WD•AD=
WD•AD= ,
,则公共部分的面积=S△ADW+S△AB′W=
 .
.故答案为
 .
.点评:本题利用了正方形的性质,三角形的面积公式,勾股定理求解.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目