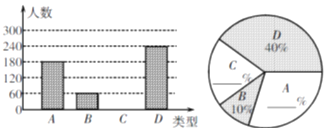
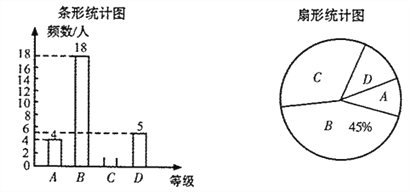
��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���![]() Ϊ����ԭ�㣬
Ϊ����ԭ�㣬![]() �Ķ���
�Ķ���![]() ��
��![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��![]() ������
������![]() ��
��![]() ����������ϣ�
����������ϣ�![]() �ĸ�
�ĸ�![]() ���߶�
���߶�![]() �ڵ�
�ڵ�![]() ����
����![]() .
.
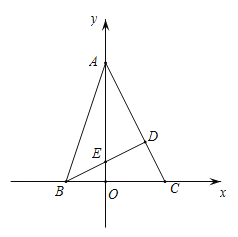
��1�����߶�![]() �ij���
�ij���
��2������![]() �ӵ�
�ӵ�![]() �������߶�
�������߶�![]() ��ÿ��
��ÿ��![]() ����λ���ȵ��ٶ����յ�
����λ���ȵ��ٶ����յ�![]() �˶�������
�˶�������![]() �ӵ�
�ӵ�![]() ����������
����������![]() ��ÿ��
��ÿ��![]() ����λ���ȵ��ٶ��˶���
����λ���ȵ��ٶ��˶���![]() ��
��![]() ����ͬʱ�������ҵ�
����ͬʱ�������ҵ�![]() ����
����![]() �㴦ʱ
�㴦ʱ![]() ��
��![]() ����ͬʱֹͣ�˶������
����ͬʱֹͣ�˶������![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() �룬
�룬![]() �����Ϊ
�����Ϊ![]() �����ú�
�����ú�![]() ��ʽ�ӱ�ʾ
��ʽ�ӱ�ʾ![]() ��ֱ��д����Ӧ��
��ֱ��д����Ӧ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3���ڣ�2���������£���![]() ��ֱ��
��ֱ��![]() �ϵ�һ����
�ϵ�һ����![]() ���Ƿ����
���Ƿ����![]() ֵ��ʹ�Ե�
ֵ��ʹ�Ե�![]() ��
��![]() ��
��![]() Ϊ��������������Ե�
Ϊ��������������Ե�![]() ��
��![]() ��
��![]() Ϊ�����������ȫ�ȣ������ڣ����������������
Ϊ�����������ȫ�ȣ������ڣ����������������![]() ֵ���������ڣ���˵������.
ֵ���������ڣ���˵������.
���𰸡���1��5����2������Q���߶�BO��ʱ��0��t��![]() ������Q���߶�BO���ӳ�����ʱ��
������Q���߶�BO���ӳ�����ʱ��![]() ��t��5����3�����ڣ�����F���߶�AC���ӳ�����ʱ��t=1������F���߶�AC��ʱ��t=
��t��5����3�����ڣ�����F���߶�AC���ӳ�����ʱ��t=1������F���߶�AC��ʱ��t=![]() ��
��
��������
��1����֤��OAC=��CBD������֤����AED�ա�BCD���ɵ�AE=BC�����ɽ��⣻
��2���������ۣ��ٵ���Q���߶�BO��ʱ������S=![]() PEOQ���ɽ��⣻
PEOQ���ɽ��⣻
�ڵ���Q���߶�BO���ӳ�����ʱ������S=![]() PEOQ���ɽ��⣻
PEOQ���ɽ��⣻
��3��������������ٵ���F���߶�AC���ӳ�����ʱ����t�ֱ��ʾPE��QC������PE=QC�������t��ֵ�����ɽ��⣬
�ڵ���F���߶�AC��ʱ����ͼ4������F��D�غϣ���t�ֱ��ʾPE��QC������PE=QC�������t��ֵ�����ɽ��⣮
�⣺��1����BD��AC��
���ADE=��BDC=90����
���CBD+��ACB=90����
�ߡ�AOC=90����
���OAC+��ACB=90����
���OAC=��CBD��
�ڡ�AED�͡�BCD�У�
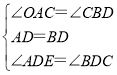 ��
��
���AED�ա�BCD��ASA����
��AE=BC��
��B��-2��0����C��3��0��
��BC=5��
��AE=5��
��2���������ۣ��ٵ���Q���߶�BO��ʱ������ͼ1��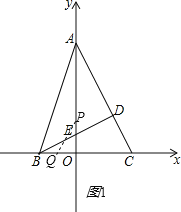
S=![]() PEOQ=
PEOQ=![]() t��2-4t��=-2t2+t����0��t��
t��2-4t��=-2t2+t����0��t��![]() ����
����
�ڵ���Q���߶�BO���ӳ�����ʱ������ͼ2��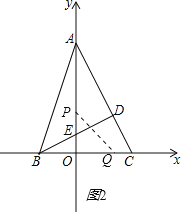
S=![]() PEOQ=
PEOQ=![]() t��4t-2��=2t2-t����
t��4t-2��=2t2-t����![]() ��t��5����
��t��5����
��3�������������
�ٵ���F���߶�AC���ӳ�����ʱ����ͼ3��
��֪��BEP=��FCQ��BE=CF����ʱ���ڡ�PBE�ա�QCF��
��PE=QC��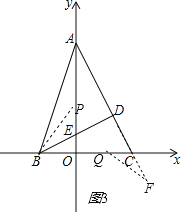
��ʱCQ=5-4t��PE=t��
��5-4t=t��
��ã�t=1��
�ڵ���F���߶�AC��ʱ����ͼ4������F��D�غϣ�
��֪��BEP=��FCQ��BE=CF����ʱ���ڡ�PBE�ա�QCF��
��PE=QC��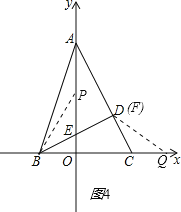
��ʱCQ=4t-5��PE=t��
��4t-5=t��
��ã�t=![]() ��
��
�ʴ�Ϊ����1��5����2������Q���߶�BO��ʱ��0��t��![]() ������Q���߶�BO���ӳ�����ʱ��
������Q���߶�BO���ӳ�����ʱ��![]() ��t��5����3�����ڣ�����F���߶�AC���ӳ�����ʱ��t=1������F���߶�AC��ʱ��t=
��t��5����3�����ڣ�����F���߶�AC���ӳ�����ʱ��t=1������F���߶�AC��ʱ��t=![]() ��
��