题目内容
 把等边△ABC沿直线l对折,使点B落在AC上得P处,AP﹕PC=1﹕2,则BE﹕BF等于
把等边△ABC沿直线l对折,使点B落在AC上得P处,AP﹕PC=1﹕2,则BE﹕BF等于
- A.1:2
- B.2:3
- C.3:4
- D.4:5
D
分析:设AP=a,BE=x,BF=y,则PC=2a,AC=3a,根据等边三角形的性质得AB=BC=AC=3a,∠ABC=∠C=∠A=60°,则根据折叠的性质得PE=BE=x,PF=BF=y,∠EPF=60°,所以∠1+∠2=120°,根据三角形内角和定理有∠1+∠3=120°,代换后得∠2=∠3,根据相似三角形的判定得到△AEP∽△CPF,则 =
= =
=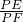 ,即
,即 =
= =
= ,根据比例性质有3ay-xy=2ax,ay=3ax-xy,变形得到4ay=5ax,所以x:y=4:5.
,根据比例性质有3ay-xy=2ax,ay=3ax-xy,变形得到4ay=5ax,所以x:y=4:5.
解答:如图,
设AP=a,BE=x,BF=y,则PC=2a,AC=3a,
∵△ABC为等边三角形,
∴AB=BC=AC=3a,∠ABC=∠C=∠A=60°,
∴AE=3a-x,CF=3a-y,
∵等边△ABC沿直线l对折,使点B落在AC上得P处,
∴PE=BE=x,PF=BF=y,∠EPF=60°,
∴∠1+∠2=120°,
∵∠1+∠3=120°,
∴∠2=∠3,
∴△AEP∽△CPF,
∴ =
= =
=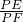 ,即
,即 =
= =
= ,
,
∴3ay-xy=2ax①,ay=3ax-xy②,
①+②得4ay=5ax,
∴x:y=4:5,
即BE﹕BF=4:5.
故选D.
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了等边三角形性质和相似三角形的判定与性质.
分析:设AP=a,BE=x,BF=y,则PC=2a,AC=3a,根据等边三角形的性质得AB=BC=AC=3a,∠ABC=∠C=∠A=60°,则根据折叠的性质得PE=BE=x,PF=BF=y,∠EPF=60°,所以∠1+∠2=120°,根据三角形内角和定理有∠1+∠3=120°,代换后得∠2=∠3,根据相似三角形的判定得到△AEP∽△CPF,则
 =
= =
=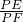 ,即
,即 =
= =
= ,根据比例性质有3ay-xy=2ax,ay=3ax-xy,变形得到4ay=5ax,所以x:y=4:5.
,根据比例性质有3ay-xy=2ax,ay=3ax-xy,变形得到4ay=5ax,所以x:y=4:5.解答:如图,

设AP=a,BE=x,BF=y,则PC=2a,AC=3a,
∵△ABC为等边三角形,
∴AB=BC=AC=3a,∠ABC=∠C=∠A=60°,
∴AE=3a-x,CF=3a-y,
∵等边△ABC沿直线l对折,使点B落在AC上得P处,
∴PE=BE=x,PF=BF=y,∠EPF=60°,
∴∠1+∠2=120°,
∵∠1+∠3=120°,
∴∠2=∠3,
∴△AEP∽△CPF,
∴
 =
= =
=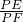 ,即
,即 =
= =
= ,
,∴3ay-xy=2ax①,ay=3ax-xy②,
①+②得4ay=5ax,
∴x:y=4:5,
即BE﹕BF=4:5.
故选D.
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了等边三角形性质和相似三角形的判定与性质.

练习册系列答案
相关题目
 17、已知等边△ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点Bˊ处,
17、已知等边△ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点Bˊ处, 把等边△ABC沿直线l对折,使点B落在AC上得P处,AP﹕PC=1﹕2,则BE﹕BF等于( )
把等边△ABC沿直线l对折,使点B落在AC上得P处,AP﹕PC=1﹕2,则BE﹕BF等于( ) 如图,已知等边△ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点Bˊ处,DBˊ,EBˊ分别交边AC于点F,G,若∠ADF=80°,则∠CEG的度数为( )
如图,已知等边△ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点Bˊ处,DBˊ,EBˊ分别交边AC于点F,G,若∠ADF=80°,则∠CEG的度数为( )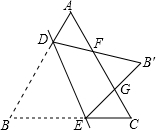 已知等边△ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在B′处,DB′,EB′分别交于AC于点F,G.若∠ADF=70°,则∠BED的度数为
已知等边△ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在B′处,DB′,EB′分别交于AC于点F,G.若∠ADF=70°,则∠BED的度数为