题目内容
 如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,DE=1.7cm,则BE=
如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,DE=1.7cm,则BE=0.8cm
0.8cm
.分析:求出∠E=∠ADC=∠BCA=90°,求出∠BCE=∠CAD,根据AAS证△ACD≌△CBE,推出CE=AD=2.5cm,BE=CD,即可得出答案.
解答:解:∵∠ACB=90°,BE⊥CE,AD⊥CE,
∴∠E=∠ADC=∠BCA=90°,
∴∠BCE+∠ACD=90°,∠ACD+∠CAD=90°,
∴∠BCE=∠CAD,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
∴CE=AD=2.5cm,BE=CD,
∵DE=1.7cm,
∴BE=CD=2.5cm-1.7cm=0.8cm,
故答案为:0.8cm.
∴∠E=∠ADC=∠BCA=90°,
∴∠BCE+∠ACD=90°,∠ACD+∠CAD=90°,
∴∠BCE=∠CAD,
在△ACD和△CBE中,
|
∴△ACD≌△CBE(AAS),
∴CE=AD=2.5cm,BE=CD,
∵DE=1.7cm,
∴BE=CD=2.5cm-1.7cm=0.8cm,
故答案为:0.8cm.
点评:本题考查了三角形的内角和定理,全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.全等三角形的对应边相等,对应角相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
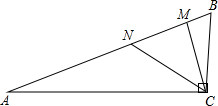 如图,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长是
如图,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长是 10、如图,∠ACB=90°,AC=BC,AE⊥CE于E,BD⊥CE于D,AE=5cm,BD=2cm,则DE的长是( )
10、如图,∠ACB=90°,AC=BC,AE⊥CE于E,BD⊥CE于D,AE=5cm,BD=2cm,则DE的长是( ) 如图,∠ACB=90°,CD⊥AB,垂足为D,下列结论错误的是( )
如图,∠ACB=90°,CD⊥AB,垂足为D,下列结论错误的是( ) 如图,∠ACB=90°,AC=BC,D为AB上一点,AE⊥CD,BF⊥CD,交CD延长线于F点.求证:BF=CE.
如图,∠ACB=90°,AC=BC,D为AB上一点,AE⊥CD,BF⊥CD,交CD延长线于F点.求证:BF=CE. 如图,∠ACB=90°,AC=AD,DE⊥AB,求证:△CDE是等腰三角形.
如图,∠ACB=90°,AC=AD,DE⊥AB,求证:△CDE是等腰三角形.