Question

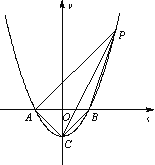
【题目】如图，已知抛物线与轴交于、两点，与轴交于点．

⑴ 求、、三点的坐标．

⑵ 过点作交抛物线于点，求四边形的面积．

⑶ 在轴上方的抛物线上是否存在一点，过作轴于点， 使以、、三点为顶点的三角形与相似．若存在，请求出点的坐标；否则，请说明理由．

Answer 1

【答案】(1)（2）;(3).

【解析】

试题分析：(1)令可分别求出的坐标；（2）对四边形的面积进行分割成再分别求解；（3）假设存在，分为直角两种情况讨论，利用相似求解.

试题解析:⑴，，

⑵ ∵ ∴

∵ ∴．

过点作轴于，则为等腰直角三角形．

令，则．∴．

∵点在抛物线上．

∴ 解得，（不合题意，舍去）∴．

∴四边形的面积．

⑶ 假设存在

∵ ∴．

∵轴于点，∴．

在中， ∴

在中， ∴

设点的横坐标为，则

①点在轴左侧时，则．

（ⅰ）当时，有．

∵，．即．解得（舍去）（舍去）．

（ⅱ）当时，有，即．

解得：（舍去）． ∴

② 点在轴右侧时，则．

（ⅰ）当时有．

∵，∴，

解得（舍去），．∴

（ⅱ）当时有．即．

解得：（舍去）．∴

∴存在点，使以、、三点为顶点的三角形与相似．

点的坐标为，，．