题目内容
把一副三角板的两个直角三角形如图叠放在一起，则∠α的度数是（ ）| A、75° | B、105° |
| C、120° | D、135° |
考点：三角形内角和定理
专题：
分析：先根据三角板的性质得出∠1及∠2的度数，再由三角形内角和定理即可得出结论．
解答：
解：∵图中是一副直角三角板，
∴∠1=45°，∠2=30°，
∴∠α=180°-45°-30°=105°．
故选B．
解：∵图中是一副直角三角板，∴∠1=45°，∠2=30°，
∴∠α=180°-45°-30°=105°．
故选B．
点评：本题考查的是三角形内角和定理，熟知三角形内角和是180°是解答此题的关键．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
一个圆锥的侧面积是底面积的2倍，则圆锥侧面展开图的扇形的圆心角是（ ）
| A、120° | B、150° |
| C、180° | D、240° |
点（4，-1）关于y轴对称的点的坐标是（ ）
| A、（-4，-1） |
| B、（-4，1） |
| C、（4，1） |
| D、（-1，4） |
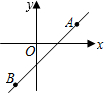如图，直线y=kx+b经过A（2，1），B（-1，a）两点，则不等式