题目内容
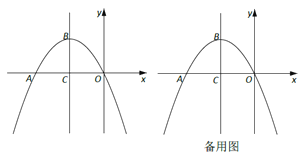
【题目】如图，在平面直角坐标系xOy中，抛物线
与x轴负半轴交于点A，顶点为B，且对称轴与x轴交于点C。
(1)求点B的坐标（用含m的代数式表示）；
(2)D为BD中点，直线AD交y轴于E，若点E的坐标为（0,2），求抛物线的解析式；
(3)在(2)的条件下，点M在直线BO上，且使得△AMC的周长最小，P在抛物线上，Q在直线BC上，若以A、M、P、Q为顶点的四边形是平行四边形，求点P的坐标。
【答案】（1）（
，- 
）；（2）
；（3）P1(1, 
)、P2(-7， 
)、P3(-5, 
)．
【解析】试题解析：（1）利用配方法或公式法都能求出点B的坐标．
（2）可过点D作DF⊥x轴于F，那么DF是△BOC的中位线，由此得出DF、OF、CF的长；再由△AFD∽△AOE得出的比例线段以及OE的长，即可求出m的值，由此确定函数的解析式．
（3）此题中，首先要确定点M的位置：已知“△AMC的周长最小”，那么可作点C关于直线BO的对称点C′，连接AC′与直线BO的交点即为符合条件的点M；
确定点M后，由于所求平行四边形的四顶点顺序并不确定，所以分：AM为边和AM为对角线两种情况讨论；在解答时，可根据平行四边形的对边平行且相等的特点，过P、Q作坐标轴的垂线，通过构建全等三角形来确定点P的坐标．
试题解析：（1）∵y＝
x22x＝
(x2mx+
m2) 
m2＝
(x
m)2
m，
∴抛物线的顶点B的坐标为(
m，
m)．
（2）令
x22x＝0，解得x1=0，x2=m．
∵抛物线y＝
x22x与x轴负半轴交于点A，
∴A（m，0），且m＜0．
过点span>D作DF⊥x轴于F，如图；
由D为BO中点，DF∥BC，可得CF=FO=
CO．
∴DF=
BC．
由抛物线的对称性得AC=OC．
∴AF：AO=3：4．
∵DF∥EO，
∴△AFD∽△AOE．
∴
．
由E（0，2），B(
m，
m)，得OE=2，DF=
m．
∴
．
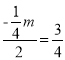∴m=-6．
∴抛物线的解析式为y＝
x22x．
（3）依题意，得A（-6，0）、B（-3，3）、C（-3，0）．可得直线OB的解析式为y=-x，直线BC为x=-3．
作点C关于直线BO的对称点C′（0，3），连接AC′交BO于M，则M即为所求．
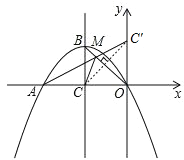
由A（-6，0），C′（0，3），可得直线AC′的解析式为y＝
x+3．
由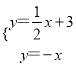
解得
∴点M的坐标为（-2，2）．
由点P在抛物线y＝
x22x上，设P（t，
t22t）．
（ⅰ）当AM为所求平行四边形的一边时．
①如图，过M作MG⊥x轴于G，过P1作P1H⊥BC于H，
则xG=xM=-2，xH=xB=-3．
∵四边形AMP1Q1为平行四边形，
∴AM=Pspan>1Q1，∠P1Q1H=∠AKC，
∵BK∥MG，
∴∠AMG=∠AKC，
∴∠P1Q1H=∠AMG，
∵
，
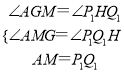∴△AMG≌△P1Q1H．
∴P1H=AG=4．
∴t-（-3）=4．
∴t=1．
∴P1(1，
)．
②如图，
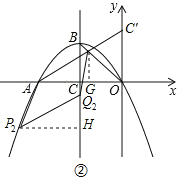
同①方法可得P2H=AG=4．
∴-3-t=4．
∴t=-7．
∴P2(7，
)．
（ⅱ）当AM为所求平行四边形的对角线时，如图；
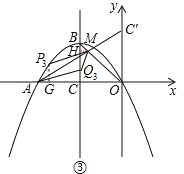
过M作MH⊥BC于H，过P3作P3G⊥x轴于G，则xH=xB=-3，xG=xP3=t．
由四边形AP3MQ3为平行四边形，可证△AP3G≌△MQ3H．
可得AG=MH=1．
∴t-（-6）=1．
∴t=-5．
∴P3(5， 
)．
综上，点P的坐标为P1(1， 
)、P2(7， 
)、P3(5， 
)．
