题目内容
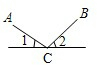如图，当∠1与∠2满足________时，AC⊥BC．
∠1+∠2=90°
分析：此题主要是利用平角及垂线的性质就可求出这个条件，由题可知当∠1与∠2满足∠1+∠2=90°时，∠ACB=180°-90°=90°∴AC⊥BC．
解答：当AC⊥BC时，∠ACB=90°
又∠1+∠ACB+∠2=180°
∴∠1+∠2=180°-∠ACB
=180°-90°=90°．
点评：此题主要考查了平角及垂线的性质即平角是180度，直角是90度．
分析：此题主要是利用平角及垂线的性质就可求出这个条件，由题可知当∠1与∠2满足∠1+∠2=90°时，∠ACB=180°-90°=90°∴AC⊥BC．
解答：当AC⊥BC时，∠ACB=90°
又∠1+∠ACB+∠2=180°
∴∠1+∠2=180°-∠ACB
=180°-90°=90°．
点评：此题主要考查了平角及垂线的性质即平角是180度，直角是90度．
练习册系列答案
科学实验活动册系列答案
相关题目
22、石山社区拟筹资金2000元，计划在一块上底，下底分别为10m，20m的梯形空地上种植花木（如图所示）．他们想在△AMD和△BMC种植单价为10元/m2的太阳花．
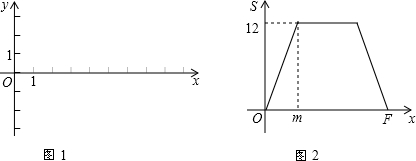
可随时打开或关闭，两水管的注水速度均为定值．当水箱注满时，两水管自动停止注水．