Question

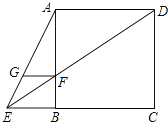
【题目】已知正方形ABC1D1的边长为1，延长C1D1到A1 ， 以A1C1为边向右作正方形A1C1C2D2 ， 延长C2D2到A2 ， 以A2C2为边向右作正方形A2C2C3D3（如图所示），以此类推…．若A1C1=2，且点A，D2 ， D3 ， …，D10都在同一直线上，则正方形A9C9C10D10的边长是 ．

Answer 1

【答案】
【解析】解：延长D4A和C1B交于O，
∵AB∥A2C1 ，
∴△AOB∽△D2OC2 ，
∴ = ，
∵AB=BC1=1，D C2=C1C2=2，
∴ = =
∴OC2=2OB，
∴OB=BC2=3，
∴OC2=6，
设正方形A2C2C3D3的边长为x1 ，
同理证得：△D2OC2∽△D3OC3 ，
∴ = ，解得，x1=3，
∴正方形A2C2C3D3的边长为3，
设正方形A3C3C4D4的边长为x2 ，
同理证得：△D3OC3∽△D4OC4 ，
∴ = ，解得x2= ，
∴正方形A3C3C4D4的边长为 ；
设正方形A4C4C5D5的边长为x3 ，
同理证得：△D4OC4∽△D5OC5 ，
∴ = ，解得x= ，
∴正方形A4C4C5D5的边长为 ；
以此类推…．
正方形An﹣1Cn﹣1CnDn的边长为 ；
∴正方形A9C9C10D10的边长为 ．
故答案为 ．
延长D4A和C1B交于O，根据正方形的性质和三角形相似的性质即可求得各个正方形的边长，从而得出规律，即可求得正方形A9C9C10D10的边长．