题目内容
如图,已知反比例函数y1 = (k1 >0)与一次函数y2 =k2 x2+1(k2≠0)相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,且tan∠AOC=2.
(k1 >0)与一次函数y2 =k2 x2+1(k2≠0)相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,且tan∠AOC=2.
(1)求出反比例函数与一次函数的解析式;
 (2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值?
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值?
(1)在Rt△OAC中,设OC= .………1分
.………1分
∵tan∠AOC=AC÷OC=2,∴AC=2×OC=2 .
. ………1分
………1分
∵ ,∴
,∴ ,
,
 ∴
∴ 或
或 (舍去).∴
(舍去).∴ ,…1分
,…1分
∴A点的坐标为(1,2). ………1分
把A点的坐标代入 中,得
中,得 .
.
∴反比例函数的表达式为 .……1分
.……1分
把A点的坐标代入 中,得
中,得 ,
,
∴一次函数的表达式 ;………1分
;………1分
(2)B点的坐标为(-2,-1).………2分
当 或
或 时,
时, .………2分
.………2分

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
| |
①若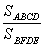 =
=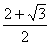 ,则tan∠EDF=
,则tan∠EDF=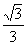 ;
;
②若DE2=BD﹒EF,则DF=2AD.
那么,下面判断正确的是
A.①是真命题,②是真命题 B.①是真命题,②是假命题
C.①是假命题,②是真命题 D.①假命题,②假命题
若二次函数y=ax2+bx+c的x与y的部分对应值如下表:
| x | ﹣7 | ﹣6 | ﹣5 | ﹣4 | ﹣3 | ﹣2 |
| y | ﹣27 | ﹣13 | ﹣3 | 3 | 5 | 3 |
则当x=﹣1时,y的值为( )
A. 5 B. ﹣3 C. ﹣13 D. ﹣27
﹣13 D. ﹣27
 B.
B.
 D.
D.
 )2-6sin300-(
)2-6sin300-( )0+
)0+ +︱
+︱ -
- ︱;
︱; D. 1
D. 1 B.
B.  C. 3a3(-2a2)=-6a5 D.
C. 3a3(-2a2)=-6a5 D. 
 的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4,P是坐标平面上的点,且以点B、O、E、P为顶点的四边形是平行四边形,则满足条件的P点坐标是 .
的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4,P是坐标平面上的点,且以点B、O、E、P为顶点的四边形是平行四边形,则满足条件的P点坐标是 .