题目内容
 如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为________.
如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为________.
16
分析:根据已知及全等三角形的判定可得到△ABC≌△CDE,从而得到b的面积=a的面积+c的面积.
解答: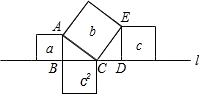 解:∵∠ACB+∠ECD=90°,∠DEC+∠ECD=90°
解:∵∠ACB+∠ECD=90°,∠DEC+∠ECD=90°
∴∠ACB=∠DEC
∵∠ABC=∠CDE,AC=CE,
在△ABC和△CDE中,
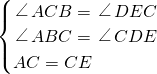
∴△ABC≌△CDE(AAS),
∴BC=DE
∴(如上图),根据勾股定理的几何意义,b的面积=a的面积+c的面积
∴b的面积=a的面积+c的面积=5+11=16.
点评:本题考查了对勾股定理几何意义的理解能力,根据三角形全等找出相等的量是解答此题的关键.
分析:根据已知及全等三角形的判定可得到△ABC≌△CDE,从而得到b的面积=a的面积+c的面积.
解答:
 解:∵∠ACB+∠ECD=90°,∠DEC+∠ECD=90°
解:∵∠ACB+∠ECD=90°,∠DEC+∠ECD=90°∴∠ACB=∠DEC
∵∠ABC=∠CDE,AC=CE,
在△ABC和△CDE中,
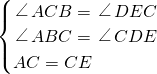
∴△ABC≌△CDE(AAS),
∴BC=DE
∴(如上图),根据勾股定理的几何意义,b的面积=a的面积+c的面积
∴b的面积=a的面积+c的面积=5+11=16.
点评:本题考查了对勾股定理几何意义的理解能力,根据三角形全等找出相等的量是解答此题的关键.

练习册系列答案
相关题目
 如图,直线l上有三个正方形a,b,c,若a,c的面积分别为7和13,则b的面积为( )
如图,直线l上有三个正方形a,b,c,若a,c的面积分别为7和13,则b的面积为( )| A、20 | ||
B、2
| ||
| C、91 | ||
D、
|

 如图,直线l上有三个正方形a,b,c,若a,b的面积分别为13和21,则c的面积为( )
如图,直线l上有三个正方形a,b,c,若a,b的面积分别为13和21,则c的面积为( ) 如图,直线l上有三个正方形a,b,c,若a,b的面积分别为5和11,则c的面积为( )
如图,直线l上有三个正方形a,b,c,若a,b的面积分别为5和11,则c的面积为( ) 如图,直线l上有三个正方形a,b,c,若a,c的面积分别为6和9,则b的面积为( )
如图,直线l上有三个正方形a,b,c,若a,c的面积分别为6和9,则b的面积为( )