题目内容
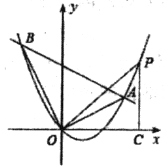
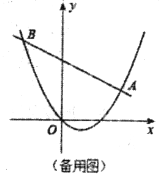
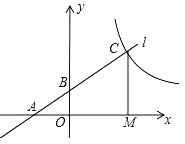
【题目】已知：如图，直线l经过点A（﹣2，0）和点B（0，1），点M在x轴上，过点M作x轴的垂线交直线l于点C，若OM＝2OA，则经过点C的反比例函数表达式为（ ）
A.y＝
B.y＝
C.y＝
D.y＝
【答案】C
【解析】
设直线l的解析式为y＝kx+b，列方程组求得y＝
x+1，根据已知条件得到点C(3，4)，设反比例函数表达式为y＝
，把C的坐标代入即可得到结论．
设直线l的解析式为：y＝kx+b，
∵直线l经过点A(﹣2，0)和点B(0，1)，
∴
，
解得：
，
∴直线l的解析式为：y＝x+1，
∵点A(﹣2，0)，
∴OA＝2，
∵OM＝2OA，
∴OM＝4，
∴点C的横坐标为4，
当x＝4时，y＝3，
∴点C(3，4)，
设反比例函数表达式为y＝，
∴m＝12，
∴反比例函数表达式为y＝
，
故选C．
练习册系列答案
口算题天天练系列答案
相关题目
【题目】某体育用品商店购进了足球和排球共20个，一共花了1360元，进价和售价如表：
足球 | 排球 | |
进价（元/个） | 80 | 50 |
售价（元/个） | 95 | 60 |
（l）购进足球和排球各多少个？
（2）全部销售完后商店共获利润多少元？
